Question

The potential energy in the joule of a particle of mass 1 kg moving in x-y plane obeys the law,\[\phi =3x+4y\] . Here x and y are in meters. If the particle is at rest at (6m, 8m) at time\[t=0\], then, the work done by the conservative force on the particle from the initial position to the instant when it crosses the x-axis is:
A. 25 J
B. -25 J
C. 50 J
D. -50 J

Answer 1

Hint: In the beginning, the particle was at rest, thus, the particle will move in the direction of the force. As the particle crosses the x-axis at the origin, thus, the sum of the initial kinetic energy and the internal energy equals the sum of the final kinetic energy and the internal energy. Using this, we will find the value of the work done.
Formula used:
\[\overset{\to }{\mathop{F}}\,=-\left( \dfrac{\partial \phi }{\partial x}i+\dfrac{\partial \phi }{\partial y}j \right)\]

Complete answer:
From the given information, we have the data as follows.
The potential energy in the joule of a particle of mass 1 kg moving in x-y plane obeys the law,\[\phi =3x+4y\] . The particle is at rest at (6m, 8m) at time\[t=0\].
The force is given as follows.
\[\overset{\to }{\mathop{F}}\,=-\left( \dfrac{\partial \phi }{\partial x}i+\dfrac{\partial \phi }{\partial y}j \right)\]
The component of ‘i’ represents the x-coordinate and the component of ‘j’ represents the y-coordinate.
Substitute the values in the above formula.
\[\begin{align}
  & \overset{\to }{\mathop{F}}\,=-\left( 3i+4j \right) \\
 & \therefore \overset{\to }{\mathop{F}}\,=-3i-4j \\
\end{align}\]
The diagrammatic representation of these values is given as follows.

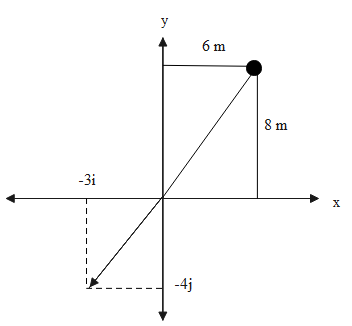
As the particle crosses the x-axis at origin, thus, the sum of the initial kinetic energy and the initial internal energy equals the sum of the final kinetic energy and the final internal energy. The mathematical representation of the same is,
\[K{{E}_{i}}+{{U}_{i}}=K{{E}_{f}}+{{U}_{f}}\]
Substitute the values in the above formula.
\[\begin{align}
  & 0+(3\times 6+4\times 8)=K{{E}_{f}}+(3\times 0+4\times 0) \\
 & \Rightarrow K{{E}_{f}}=18+32 \\
 & \therefore K{{E}_{f}}=50\,J \\
\end{align}\]
\[\therefore \] The work done by the conservative force on the particle from the initial position to the instant when it crosses the x-axis is 50 J.

Thus, option (C) is correct.

Note:
In the beginning, the particle was at rest, thus, the particle will move in the direction of the force. As the particle crosses the x-axis at the origin, thus, the sum of the initial kinetic energy and the internal energy equals the sum of the final kinetic energy and the internal energy.