
The position time graph for motion with zero acceleration is:
A.)
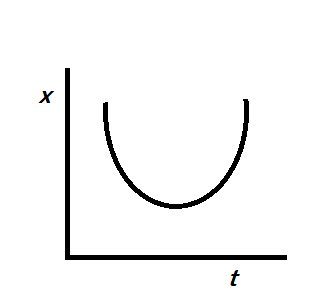
B.)
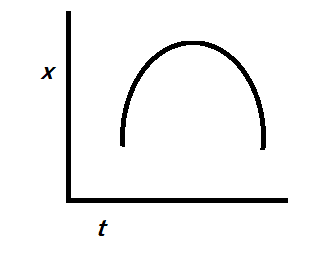
C.)
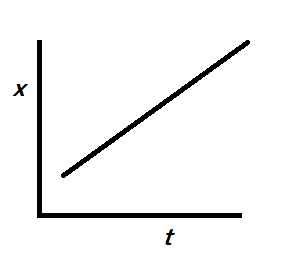
D.)
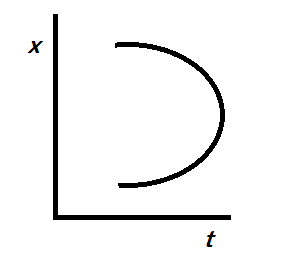
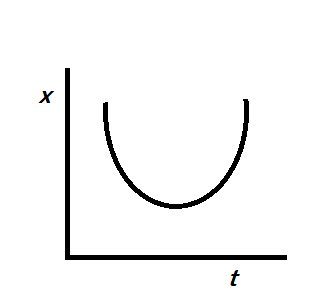
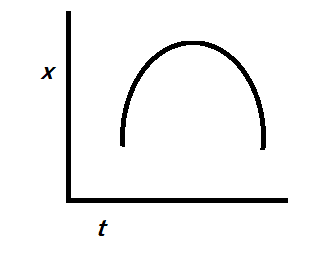
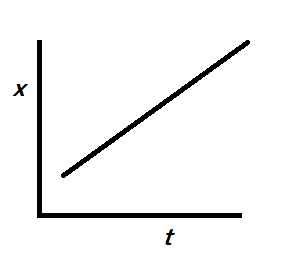
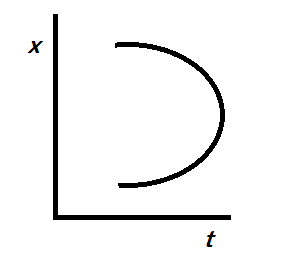
Answer
584.4k+ views
Hint: We know that acceleration is how fast or slow the velocity is with respect to time.This differentiation is nothing but the slope of the graph. Hence we must take the slope of the given curves to find the correct option, among the following.
Formula used:
$a=\dfrac{dv}{dt}=\dfrac{d^{2}x}{dt^{2}}$
Complete answer:
We know that velocity is the rate of change of displacement with respect to time. It is mathematically denoted as $v=\dfrac{dx}{dt}$. This is nothing but the slope of the x-t graph.
Similarly, acceleration is the rate of change of velocity with respect to time. It is mathematically denoted as $a=\dfrac{dv}{dt}$. This is nothing but the slope of the v-t graph.
Given that acceleration is zero, or $a=\dfrac{dv}{dt}=0$, this happens when velocity is a constant . i.e. velocity is independent of time and its slope is $0$.
Since we know from mathematics, that $\dfrac{d}{dx}k=0$
Then the v-t graph is given as:
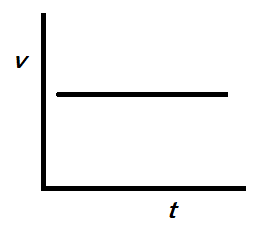
Then for $v$ to be a constant with respect to time we can say that the x-t graph is linear. Like $k\times x$ this is because we know that $\dfrac{d}{dx}kx=k$.
Since the x-t graph must be linear, in the given options, only C is linear and the other options are not linear i.e. specifically quadratic here.
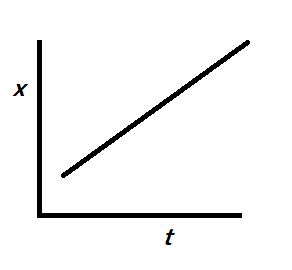
So, the correct answer is “Option C”.
Note:
Here, the answer is discussed in the form of derivation of simplicity. However one can integrate $a=\dfrac{dv}{dt}=0$ twice, to reach the same answer. It is important to know either integration or differentiation to solve this sum. Also note that the slope of the x-t graph is nothing but the velocity and the slope of the v-t graph is the acceleration.
Formula used:
$a=\dfrac{dv}{dt}=\dfrac{d^{2}x}{dt^{2}}$
Complete answer:
We know that velocity is the rate of change of displacement with respect to time. It is mathematically denoted as $v=\dfrac{dx}{dt}$. This is nothing but the slope of the x-t graph.
Similarly, acceleration is the rate of change of velocity with respect to time. It is mathematically denoted as $a=\dfrac{dv}{dt}$. This is nothing but the slope of the v-t graph.
Given that acceleration is zero, or $a=\dfrac{dv}{dt}=0$, this happens when velocity is a constant . i.e. velocity is independent of time and its slope is $0$.
Since we know from mathematics, that $\dfrac{d}{dx}k=0$
Then the v-t graph is given as:
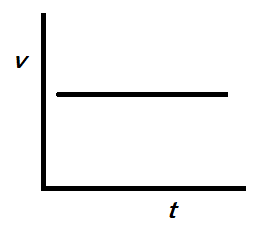
Then for $v$ to be a constant with respect to time we can say that the x-t graph is linear. Like $k\times x$ this is because we know that $\dfrac{d}{dx}kx=k$.
Since the x-t graph must be linear, in the given options, only C is linear and the other options are not linear i.e. specifically quadratic here.
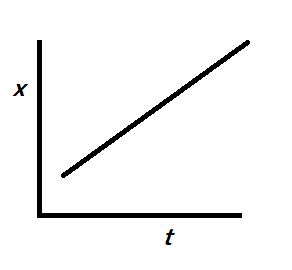
So, the correct answer is “Option C”.
Note:
Here, the answer is discussed in the form of derivation of simplicity. However one can integrate $a=\dfrac{dv}{dt}=0$ twice, to reach the same answer. It is important to know either integration or differentiation to solve this sum. Also note that the slope of the x-t graph is nothing but the velocity and the slope of the v-t graph is the acceleration.
Recently Updated Pages
The number of solutions in x in 02pi for which sqrt class 12 maths CBSE

Write any two methods of preparation of phenol Give class 12 chemistry CBSE

Differentiate between action potential and resting class 12 biology CBSE

Two plane mirrors arranged at right angles to each class 12 physics CBSE

Which of the following molecules is are chiral A I class 12 chemistry CBSE

Name different types of neurons and give one function class 12 biology CBSE

Trending doubts
One Metric ton is equal to kg A 10000 B 1000 C 100 class 11 physics CBSE

Explain zero factorial class 11 maths CBSE

What is 1s 2s 2p 3s 3p class 11 chemistry CBSE

Discuss the various forms of bacteria class 11 biology CBSE

State the laws of reflection of light

Difference Between Prokaryotic Cells and Eukaryotic Cells




