Question

The portion of a tangent to a parabola \[{{y}^{2}}=4ax\] cuts off between the directrix and the curve subtends an angle $\theta $ at the focus, where $\theta =$
A. $\dfrac{\pi }{4}$
B. $\dfrac{\pi }{3}$
C. $\dfrac{\pi }{2}$
D. None of these

Answer 1

Hint: To find the angle $\theta $ , Let us assume $x=a{{t}^{2}}$ . Hence, \[{{y}^{2}}=4ax\Rightarrow {{y}^{2}}=4{{a}^{2}}{{t}^{2}}\] . We can consider a point P on the parabola and that will be denoted as $\left( a{{t}^{2}},2at \right)$ . This point cuts the directrix at R. Let $S\left( a,0 \right)$ be the focus of the parabola. Now, find the equation of tangents to the parabola using the formula $y{{y}_{1}}=2a\left( x+{{x}_{1}} \right)$ and we will get $y=\dfrac{1}{t}x+at$ . The equation of tangent PR that intersects the directrix $x=-a$ is $y=\dfrac{1}{t}\left( -a \right)+at$ . We can write the coordinates of R as $\left( -a,\dfrac{a}{t}\left[ {{t}^{2}}-1 \right] \right)$ . Now, find the slopes of tangents PS and RS using the formula $m=\dfrac{{{y}_{2}}-{{y}_{1}}}{{{x}_{2}}-{{x}_{1}}}$ . Now, multiply these slopes to get \[{{m}_{1}}{{m}_{2}}=-1\].

Complete step-by-step solution:
It is given that the portion of a tangent to a parabola \[{{y}^{2}}=4ax\] cuts off between the directrix and the curve subtends an angle $\theta $ at the focus. We have to find the angle $\theta $.
We have \[{{y}^{2}}=4ax\] .
Let us assume $x=a{{t}^{2}}$ . Hence,
\[\begin{align}
  & {{y}^{2}}=4a\left( a{{t}^{2}} \right) \\
 & \Rightarrow {{y}^{2}}=4{{a}^{2}}{{t}^{2}} \\
\end{align}\]
Let us take the square root of the above equation. We will get
\[y=2at\]
Hence, we can consider a point P on the parabola and that will be denoted as $\left( a{{t}^{2}},2at \right)$ .
Let us draw the diagram.

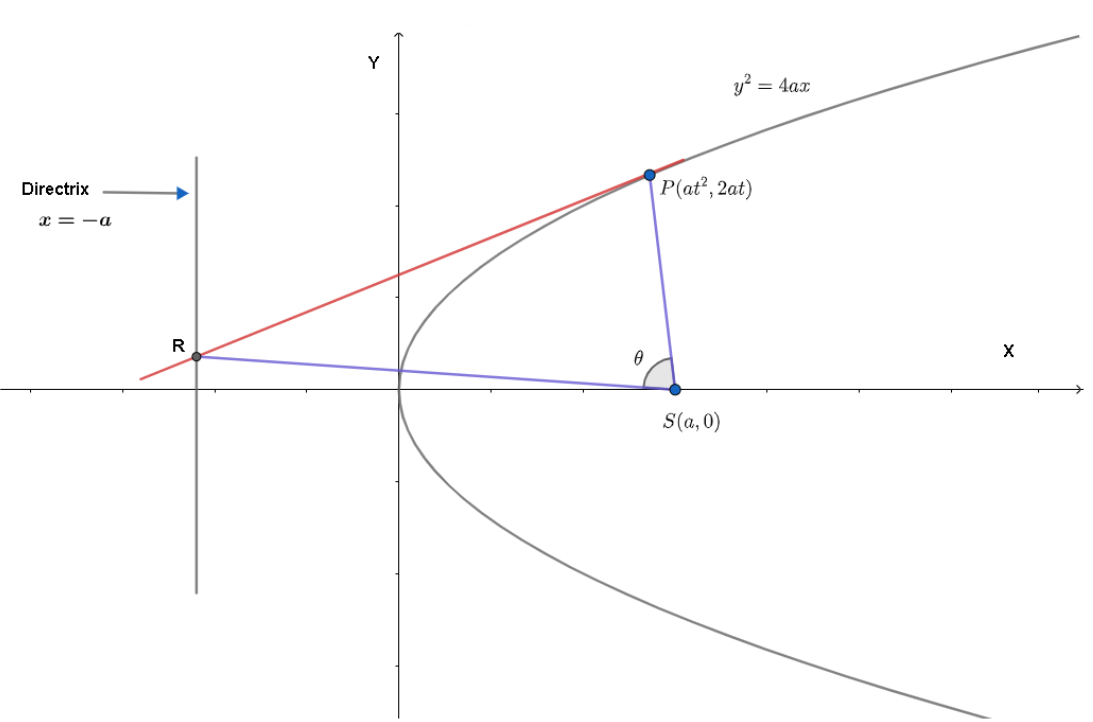
From the figure, we can see that the red color shows the tangent that cuts the directrix at R.
We know that equation of the tangent to the parabola \[{{y}^{2}}=4ax\] at a point $\left( {{x}_{1}},{{y}_{1}} \right)$ is $y{{y}_{1}}=2a\left( x+{{x}_{1}} \right)$
Hence, we can find the equation of tangent to the parabola \[{{y}^{2}}=4ax\] at a point $P\left( a{{t}^{2}},2at \right)$ and is given as
$y\times 2at=2a\left( x+a{{t}^{2}} \right)$
Let us cancel the common terms from both sides. We will get
$\begin{align}
  & yt=x+a{{t}^{2}} \\
 & \Rightarrow y=\dfrac{x+a{{t}^{2}}}{t} \\
\end{align}$
By solving this, we will get
$y=\dfrac{1}{t}x+at$
Now, we can get the equation of tangent PR that intersects directrix $x=-a$ and is shown below.
$y=\dfrac{1}{t}\left( -a \right)+at$
Let us take $\dfrac{a}{t}$ outside from this equation. We will get
$y=\dfrac{a}{t}\left[ {{t}^{2}}-1 \right]$
Hence, we can write the coordinates of R as $\left( -a,\dfrac{a}{t}\left[ {{t}^{2}}-1 \right] \right)$ .
Let us find the slope of the tangent PS.
We know that slope of a tangent is given by
$m=\dfrac{{{y}_{2}}-{{y}_{1}}}{{{x}_{2}}-{{x}_{1}}}$
Thus, we can find the slope of PS as
\[{{m}_{1}}=\dfrac{2at-0}{a{{t}^{2}}-a}\]
\[\Rightarrow {{m}_{1}}=\dfrac{2at}{a\left( {{t}^{2}}-1 \right)}\]
When we cancel the common terms, we will get
\[{{m}_{1}}=\dfrac{2t}{\left( {{t}^{2}}-1 \right)}...(i)\]
Now, let us find the slope of RS.
\[\Rightarrow {{m}_{2}}=\dfrac{\dfrac{a}{t}\left[ {{t}^{2}}-1 \right]-0}{-a-a}\]
\[\Rightarrow {{m}_{2}}=\dfrac{\dfrac{a}{t}\left[ {{t}^{2}}-1 \right]}{-2a}\]
Let us solve this. When we cancel the common terms, we will get
\[{{m}_{2}}=\dfrac{-\left[ {{t}^{2}}-1 \right]}{2t}...(ii)\]
Let us multiply (i) and (ii).
\[\Rightarrow {{m}_{1}}{{m}_{2}}=\dfrac{2t}{\left( {{t}^{2}}-1 \right)}\times \dfrac{-\left[ {{t}^{2}}-1 \right]}{2t}\]
Let us cancel the common terms. We will get
\[\Rightarrow {{m}_{1}}{{m}_{2}}=-1\]
We know that two lines are perpendicular if the product of their slopes is equal to -1.
Hence, lines PS and RS are perpendicular.
Hence, the angle between them will be $\theta =\dfrac{\pi }{2}$. Hence, the correct option is C.

Note: We must draw the diagram to proceed further with the solution. We drew the parabola on the right of the origin as the equation was \[{{y}^{2}}=4ax\]. If the equation of the parabola was \[{{y}^{2}}=-4ax\], the parabola will be to the left of the origin. You may make mistake when writing the formula $y{{y}_{1}}=2a\left( x+{{x}_{1}} \right)$ as $x{{x}_{1}}=2a\left( y+{{y}_{1}} \right)$ . Also, you may write the formula to find the slope as $m=\dfrac{{{x}_{2}}-{{x}_{1}}}{{{y}_{2}}-{{y}_{1}}}$. So for solving these problems we should have a brief knowledge of formulas otherwise a small mistake will give the wrong answer.