Question

The points \[{z_1},{z_2},{z_3},{z_4}\], in the complex plane are the vertices of a parallelogram taken in order, if and only if
1) \[{z_1} + {z_4} = {z_2} + {z_3}\]
2) \[{z_1} + {z_3} = {z_2} + {z_4}\]
3) \[{z_1} + {z_2} = {z_3} + {z_4}\]
4) None of these

Answer 1

Hint: This question requires the knowledge of parallelogram. If one is aware about the condition for which the quadrilateral is considered as a parallelogram, then the question is easy. The condition is: \[ \Rightarrow \dfrac{{{z_1} + {z_3}}}{2} = \dfrac{{{z_2} + {z_4}}}{2}\]
As the mid-points are common, the diagonals of a parallelogram lie on the same point. We must know that the diagonals of a parallelogram bisect each other to attempt such questions

Complete step-by-step answer:
We know that the diagonals of a parallelogram bisect each other. This means that the intersection of the two diagonals of a parallelogram is the midpoint of both the diagonals.
Thus, applying the above condition to create a parallelogram in the imaginary plane,

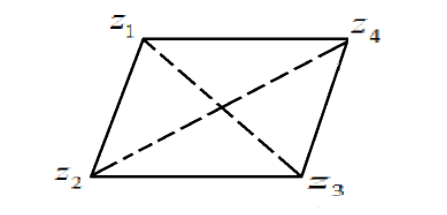
Now, we know the midpoint formula. So, the coordinates of the midpoint of a line segment are the arithmetic mean of the coordinates of the endpoints of the line segment. Also, the midpoints of the two diagonals of a parallelogram are the same.
Now, we also know the midpoint of line formed by joining two complex numbers on argand plane is given by the arithmetic mean of the two complex numbers as $\left( {\dfrac{{a + b}}{2}} \right)$. Hence, we have,
\[ \Rightarrow \dfrac{{{z_1} + {z_3}}}{2} = \dfrac{{{z_2} + {z_4}}}{2}\]
Multiplying, 2 on both sides of the equation we get,
\[ \Rightarrow {z_1} + {z_3} = {z_2} + {z_4}\]
Hence, this is the condition for the points to be the vertices of the parallelogram.
So, the correct answer is “Option 2”.

Note: In Euclidean geometry, a parallelogram is a simple quadrilateral with two pairs of parallel sides. The opposite or facing sides of a parallelogram are of equal length and the opposite angles of a parallelogram are of equal measure