Question

The points $A\left( {{x}_{1}},{{y}_{1}} \right),B\left( {{x}_{2}},{{y}_{2}} \right)$ and $C\left( {{x}_{3}},{{y}_{3}} \right)$ are the vertices of $\Delta ABC$. The median AD meets BC at D. Find the coordinates of points Q and R on medians BE and CF, respectively such that $BQ:QE=2:1$ and $CR:RF=2:1$
A. $\dfrac{2{{x}_{1}}+2{{x}_{2}}+{{x}_{3}}}{3},\dfrac{2{{y}_{1}}+2{{y}_{2}}+{{y}_{3}}}{3}$
B. $\dfrac{{{x}_{1}}+{{x}_{2}}+2{{x}_{3}}}{3},\dfrac{{{y}_{1}}+{{y}_{2}}+2{{y}_{3}}}{3}$
C. ${{x}_{1}}+{{x}_{2}}+{{x}_{3}},{{y}_{1}}+{{y}_{2}}+{{y}_{3}}$
D. $\dfrac{{{x}_{1}}+{{x}_{2}}+{{x}_{3}}}{3},\dfrac{{{y}_{1}}+{{y}_{2}}+{{y}_{3}}}{3}$

Answer 1

Hint: We first use the section ratio and concept of middle point of a line to find the coordinates of D, E, F. Then we use the formula of section ratio $\left( \dfrac{mc+na}{m+n},\dfrac{md+nb}{m+n} \right)$ for section ration of \[m:n\] for the points $\left( a,b \right),\left( c,d \right)$, to find the points Q and R. we can see the relation between those two points being similar which gives us the solution.

Complete step-by-step answer:
The points $A\left( {{x}_{1}},{{y}_{1}} \right),B\left( {{x}_{2}},{{y}_{2}} \right)$ and $C\left( {{x}_{3}},{{y}_{3}} \right)$ are the vertices of $\Delta ABC$. The median AD meets BC at D.
We can assume that the median BE meets AC at E and the median CF meets AB at F.
Now we use the section formula to find the coordinates of the points E and F.

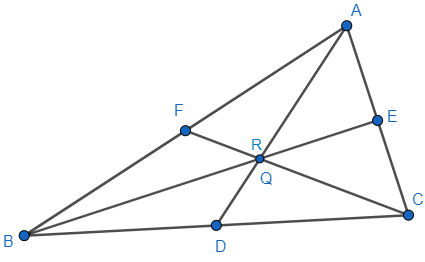
D, E, F are midpoints of the line BC, AC and AB respectively. The section ratio is \[1:1\].
The section ration of \[m:n\] for the points $\left( a,b \right),\left( c,d \right)$ will be $\left( \dfrac{mc+na}{m+n},\dfrac{md+nb}{m+n} \right)$.
So, $D=\left( \dfrac{{{x}_{2}}+{{x}_{3}}}{2},\dfrac{{{y}_{2}}+{{y}_{3}}}{2} \right)$, $E=\left( \dfrac{{{x}_{1}}+{{x}_{3}}}{2},\dfrac{{{y}_{1}}+{{y}_{3}}}{2} \right)$, $F=\left( \dfrac{{{x}_{1}}+{{x}_{2}}}{2},\dfrac{{{y}_{1}}+{{y}_{2}}}{2} \right)$.
Now points Q and R on medians BE and CF are in such a way that $BQ:QE=2:1$ and $CR:RF=2:1$ which means the section ratio of BE and CF at points Q and R is \[2:1\].
We apply the same method to find the points.
First for point Q in the line of BE will be $Q=\left( \dfrac{2\left( \dfrac{{{x}_{1}}+{{x}_{3}}}{2} \right)+{{x}_{2}}}{2+1},\dfrac{2\left( \dfrac{{{y}_{1}}+{{y}_{3}}}{2} \right)+{{y}_{2}}}{2+1} \right)=\left( \dfrac{{{x}_{1}}+{{x}_{2}}+{{x}_{3}}}{3},\dfrac{{{y}_{1}}+{{y}_{2}}+{{y}_{3}}}{3} \right)$
And for point R in the line of CF will be $R=\left( \dfrac{2\left( \dfrac{{{x}_{1}}+{{x}_{2}}}{2} \right)+{{x}_{3}}}{2+1},\dfrac{2\left( \dfrac{{{y}_{1}}+{{y}_{2}}}{2} \right)+{{y}_{3}}}{2+1} \right)=\left( \dfrac{{{x}_{1}}+{{x}_{2}}+{{x}_{3}}}{3},\dfrac{{{y}_{1}}+{{y}_{2}}+{{y}_{3}}}{3} \right)$.
So, both coordinates are similar which means both points are the same point.
The correct option is D.
So, the correct answer is “Option D”.

Note: We can’t say the relation of similarity until we have found the coordinates. The point is actually the centroid of the triangle $\Delta ABC$. The centroid of a triangle always intersects its medians at the ratio of \[2:1\] from the side of its vertices. From the above coordinates of Q and R we can say that the x and y coordinates of the centroid are equal to the sum of the x and y coordinates divided by 3. For example: for points $A\left( {{x}_{1}},{{y}_{1}} \right),B\left( {{x}_{2}},{{y}_{2}} \right)$ and $C\left( {{x}_{3}},{{y}_{3}} \right)$ the centroid became $\dfrac{{{x}_{1}}+{{x}_{2}}+{{x}_{3}}}{3},\dfrac{{{y}_{1}}+{{y}_{2}}+{{y}_{3}}}{3}$.