Question

The point of intersection of X and Y axis is called:
A . Origin
B . Null point
C . Common point
D . None of these

Answer 1

Hint: To solve the question given above, we will first see what are x-axis and y-axis. Then we will consider a variable point on x-axis and a variable point on y-axis. We will then move these points such that their distance keeps on decreasing. When the distance between them becomes zero, which will be the intersection point of these axis.

Complete step-by-step answer:
Before solving the above question, we must know what x-axis is and what y-axis is. The x-axis is a horizontal axis of a system of coordinates. X-axis contains the value of all the real numbers. The y-axis is a vertical axis of a system of coordinates. Y-axis contains the value of all the real numbers. Now, we have to find the intersection point of the axis. The intersection point is a point where both the lines meet. In other words, intersection point is a point at which both the lines give the same value.

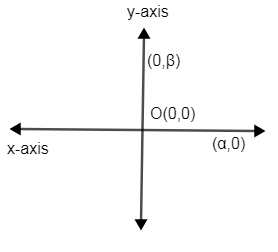
Now, we will consider a point $\alpha $ on x-axis $\left( \alpha >0 \right)$ and a point \[\beta \] on y-axis $\left( \beta >0 \right)$ . let us move $\alpha $ and $\beta $ such that the distance between them keeps on decreasing. For the distance to decrease their absolute value should decrease. Now, at point $\left( 0,0 \right)$ , the distance between them becomes zero. This point will be the intersection point of both the axes. The point $\left( 0,0 \right)$ is called the origin . Thus, the point of intersection of X and Y axes is called origin.
Hence, option (a) is correct.

Note: Similarly to x-axis and y-axis, if there had been a third axis perpendicular to both of them, say z-axis, then also the intersection point of all the axis would have been origin. We can prove it similarly by taking a point on z-axis and decreasing its distance from other two points