
The point of inflection of ${{\left( x-5 \right)}^{55}}{{\left( x-6 \right)}^{66}}$ is
A. 0
B. 5
C. 6
D. $\dfrac{660}{121}$
Answer
533.4k+ views
Hint: We first explain the process of points of inflection. We find the concept of inflection being similar to finding extremum points. The second derivative of the function gives us the solution of the problem.
Complete step by step solution:
We have to find the inflection points for $f\left( x \right)={{\left( x-5 \right)}^{55}}{{\left( x-6 \right)}^{66}}$. Inflection points are points where the function changes concavity, from being "concave up" to being "concave down" or vice versa. They can be found by considering where the second derivative changes signs.
Therefore, we have to find the second derivative of the function $f\left( x \right)={{\left( x-5 \right)}^{55}}{{\left( x-6 \right)}^{66}}$.
We take logarithm for $y={{\left( x-5 \right)}^{55}}{{\left( x-6 \right)}^{66}}$. We get $\log y=55\log \left( x-5 \right)+66\log \left( x-6 \right)$.
We know that \[\dfrac{d}{dx}\left( \log x \right)=\dfrac{1}{x}\]. We use that for the differentiation where $\log y$.
For our given function, we can differentiate it to ${{f}^{'}}\left( x \right)=\dfrac{df}{dx}$.
On first differentiation, we get
$\begin{align}
& \log y=55\log \left( x-5 \right)+66\log \left( x-6 \right) \\
& \Rightarrow \dfrac{1}{y}\dfrac{dy}{dx}=\dfrac{55}{\left( x-5 \right)}+\dfrac{66}{\left( x-6 \right)} \\
& \Rightarrow \dfrac{dy}{dx}=y\left[ \dfrac{55}{\left( x-5 \right)}+\dfrac{66}{\left( x-6 \right)} \right] \\
\end{align}$
For the second derivative of the function, we can convert it to \[{{f}^{''}}\left( x \right)=\dfrac{d\left( {{f}^{'}} \right)}{dx}\].
On second differentiation, we get
$\begin{align}
& \dfrac{dy}{dx}=y\left[ \dfrac{55}{\left( x-5 \right)}+\dfrac{66}{\left( x-6 \right)} \right] \\
& \Rightarrow \dfrac{{{d}^{2}}y}{d{{x}^{2}}}=\dfrac{dy}{dx}\left[ \dfrac{55}{\left( x-5 \right)}+\dfrac{66}{\left( x-6 \right)} \right]-y\left[ \dfrac{55}{{{\left( x-5 \right)}^{2}}}+\dfrac{66}{{{\left( x-6 \right)}^{2}}} \right] \\
\end{align}$
We know that the solution for ${{f}^{'}}\left( x \right)=y\left[ \dfrac{55}{\left( x-5 \right)}+\dfrac{66}{\left( x-6 \right)} \right]$ is $x=5,6$.
We also show the changes as
Therefore, the function changes its concavity once. The correct option is B.
We try to explain this concept with the graph also.
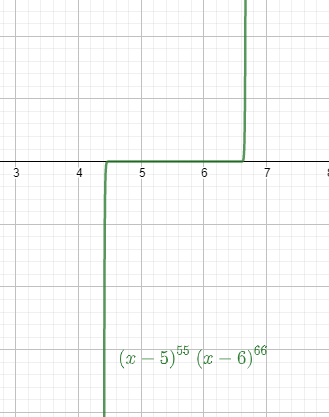
Note: We need to remember the concept of extremum and point of inflection is quite similar. The slopes decide the concavity and its change. We also need to remember that If a function is undefined at some value of x, there can be no inflection point.
Complete step by step solution:
We have to find the inflection points for $f\left( x \right)={{\left( x-5 \right)}^{55}}{{\left( x-6 \right)}^{66}}$. Inflection points are points where the function changes concavity, from being "concave up" to being "concave down" or vice versa. They can be found by considering where the second derivative changes signs.
Therefore, we have to find the second derivative of the function $f\left( x \right)={{\left( x-5 \right)}^{55}}{{\left( x-6 \right)}^{66}}$.
We take logarithm for $y={{\left( x-5 \right)}^{55}}{{\left( x-6 \right)}^{66}}$. We get $\log y=55\log \left( x-5 \right)+66\log \left( x-6 \right)$.
We know that \[\dfrac{d}{dx}\left( \log x \right)=\dfrac{1}{x}\]. We use that for the differentiation where $\log y$.
For our given function, we can differentiate it to ${{f}^{'}}\left( x \right)=\dfrac{df}{dx}$.
On first differentiation, we get
$\begin{align}
& \log y=55\log \left( x-5 \right)+66\log \left( x-6 \right) \\
& \Rightarrow \dfrac{1}{y}\dfrac{dy}{dx}=\dfrac{55}{\left( x-5 \right)}+\dfrac{66}{\left( x-6 \right)} \\
& \Rightarrow \dfrac{dy}{dx}=y\left[ \dfrac{55}{\left( x-5 \right)}+\dfrac{66}{\left( x-6 \right)} \right] \\
\end{align}$
For the second derivative of the function, we can convert it to \[{{f}^{''}}\left( x \right)=\dfrac{d\left( {{f}^{'}} \right)}{dx}\].
On second differentiation, we get
$\begin{align}
& \dfrac{dy}{dx}=y\left[ \dfrac{55}{\left( x-5 \right)}+\dfrac{66}{\left( x-6 \right)} \right] \\
& \Rightarrow \dfrac{{{d}^{2}}y}{d{{x}^{2}}}=\dfrac{dy}{dx}\left[ \dfrac{55}{\left( x-5 \right)}+\dfrac{66}{\left( x-6 \right)} \right]-y\left[ \dfrac{55}{{{\left( x-5 \right)}^{2}}}+\dfrac{66}{{{\left( x-6 \right)}^{2}}} \right] \\
\end{align}$
We know that the solution for ${{f}^{'}}\left( x \right)=y\left[ \dfrac{55}{\left( x-5 \right)}+\dfrac{66}{\left( x-6 \right)} \right]$ is $x=5,6$.
We also show the changes as
| domain of x | value of ${{f}^{'}}\left( x \right)$ | characteristics |
| $x<5$ | negative | concave down |
| $5 < x < 6$ | positive | concave up |
| $x>6$ | positive | concave up |
Therefore, the function changes its concavity once. The correct option is B.
We try to explain this concept with the graph also.

Note: We need to remember the concept of extremum and point of inflection is quite similar. The slopes decide the concavity and its change. We also need to remember that If a function is undefined at some value of x, there can be no inflection point.
Recently Updated Pages
Master Class 11 Computer Science: Engaging Questions & Answers for Success

Master Class 11 Business Studies: Engaging Questions & Answers for Success

Master Class 11 Economics: Engaging Questions & Answers for Success

Master Class 11 English: Engaging Questions & Answers for Success

Master Class 11 Maths: Engaging Questions & Answers for Success

Master Class 11 Biology: Engaging Questions & Answers for Success

Trending doubts
One Metric ton is equal to kg A 10000 B 1000 C 100 class 11 physics CBSE

There are 720 permutations of the digits 1 2 3 4 5 class 11 maths CBSE

Discuss the various forms of bacteria class 11 biology CBSE

Draw a diagram of a plant cell and label at least eight class 11 biology CBSE

State the laws of reflection of light

Explain zero factorial class 11 maths CBSE




