Question

The point $\left( 5,-7 \right)$ lies outside to which of the following circles?
(a) ${{x}^{2}}+{{y}^{2}}-8x=0$
(b) ${{x}^{2}}+{{y}^{2}}-5x+7y=0$
(c) ${{x}^{2}}+{{y}^{2}}-5x+7y-1=0$
(d) ${{x}^{2}}+{{y}^{2}}-8x+7y-2=0$

Answer 1

Hint: We start solving the problem by recalling the conditions for a point to lie inside, outside or on the circle i.e., if $S\equiv 0$ is the equation of the circle and $\left( {{x}_{1}},{{y}_{1}} \right)$ is any point and if ${{S}_{11}}=0$, then the point lies on the circle, if ${{S}_{11}}<0$, then the point lies inside the circle, if ${{S}_{11}}>0$, then the point lies outside the circle.. We then substitute the given point in each equation of the circle given in the options to check whether it is satisfying the condition or not to get the required answer.

Complete step by step answer:
According to the problem, we have given a point $\left( 5,-7 \right)$ and we need to find the equation of the circle for which this point lies outside of it from the given options.
We know that if $S\equiv 0$ is the equation of the circle and $\left( {{x}_{1}},{{y}_{1}} \right)$ is any point.
If ${{S}_{11}}=0$, then the point lies on the circle.
If ${{S}_{11}}<0$, then the point lies inside the circle.
If ${{S}_{11}}>0$, then the point lies outside the circle.
Let us check ${{S}_{11}}$ for each option by substituting the point $\left( 5,-7 \right)$ in its equation.
Let us first check option (a).
So, we have the equation of the circle as $S:{{x}^{2}}+{{y}^{2}}-8x=0$.

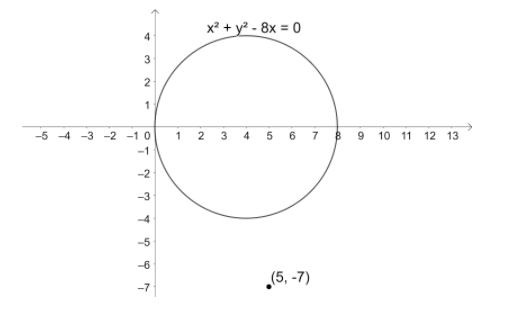
So, we have ${{S}_{11}}={{\left( 5 \right)}^{2}}+{{\left( -7 \right)}^{2}}-8\left( 5 \right)$.
$\Rightarrow {{S}_{11}}=25+49-40$.
$\Rightarrow {{S}_{11}}=34>0$.
So, the point $\left( 5,-7 \right)$ lies outside the circle ${{x}^{2}}+{{y}^{2}}-8x=0$.
So, option (a) is correct.
Let us first check option (b).
So, we have the equation of circle as $S:{{x}^{2}}+{{y}^{2}}-5x+7y=0$.

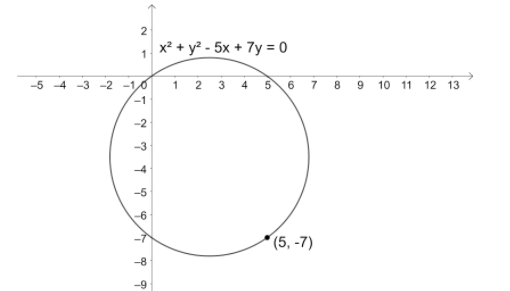
So, we have ${{S}_{11}}={{\left( 5 \right)}^{2}}+{{\left( -7 \right)}^{2}}-5\left( 5 \right)+7\left( -7 \right)$.
$\Rightarrow {{S}_{11}}=25+49-25-49$.
$\Rightarrow {{S}_{11}}=0$.
So, the point $\left( 5,-7 \right)$ lies on the circle ${{x}^{2}}+{{y}^{2}}-5x+7y=0$.
So, option (b) is not correct.
Let us first check option (c).
So, we have the equation of circle as $S:{{x}^{2}}+{{y}^{2}}-5x+7y-1=0$.

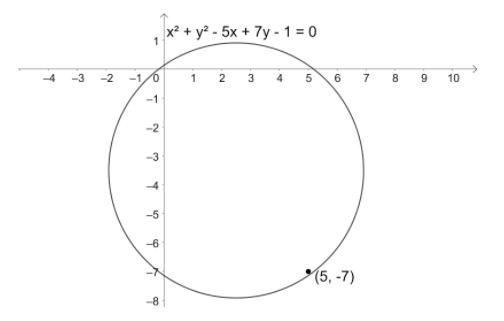
So, we have ${{S}_{11}}={{\left( 5 \right)}^{2}}+{{\left( -7 \right)}^{2}}-5\left( 5 \right)+7\left( -7 \right)-1$.
$\Rightarrow {{S}_{11}}=25+49-25-49-1$.
$\Rightarrow {{S}_{11}}=-1<0$.
So, the point $\left( 5,-7 \right)$ lies inside the circle ${{x}^{2}}+{{y}^{2}}-5x+7y-1=0$.
So, option (c) is not correct.
Let us first check option (d).
So, we have the equation of the circle as $S:{{x}^{2}}+{{y}^{2}}-8x+7y-2=0$.

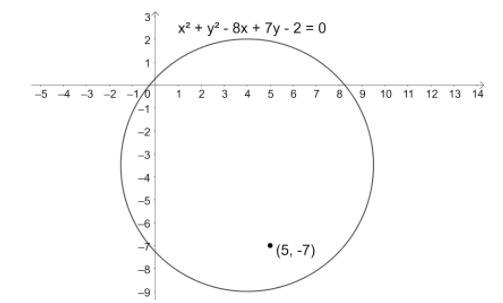
So, we have ${{S}_{11}}={{\left( 5 \right)}^{2}}+{{\left( -7 \right)}^{2}}-8\left( 5 \right)+7\left( -7 \right)-2$.
$\Rightarrow {{S}_{11}}=25+49-40-49-1$.
$\Rightarrow {{S}_{11}}=-16<0$.
So, the point $\left( 5,-7 \right)$ lies inside the circle ${{x}^{2}}+{{y}^{2}}-8x+7y-2=0$.
So, option (d) is not correct.

So, the correct answer is “Option a”.

Note: We should not confuse ${{S}_{11}}<0$ for lying outside the circle which is the most common mistake done by the students. The conditions we have just discussed for a point lying inside, outside or on the circle is valid for all conics not only for the circle. We can also solve this problem by checking whether the distance from the centre of the circle to that point is greater than the radius of the circle in order to present outside the circle. Similarly, we can expect problems to find the total number of tangents drawn from that point on to the circle.