Question

The point \[\left( {4,1} \right)\] undergoes the following 3 transformations successively:
(i)Reflection about the line \[y = x\]
(ii)Translations through a distance of 2 units along the positive direction of \[x\] axis.
(iii)Rotation through an angle \[\dfrac{\pi }{4}\] about the origin in the anti-clockwise sense.
Then the final position of the point is given by:
A.\[\left( {\dfrac{1}{{\sqrt 2 }},\dfrac{7}{{\sqrt 2 }}} \right)\]
B.\[\left( { - \sqrt 2 ,7\sqrt 2 } \right)\]
C.\[\left( { - \dfrac{1}{{\sqrt 2 }},\dfrac{7}{{\sqrt 2 }}} \right)\]
D.\[\left( {\sqrt 2 ,7\sqrt 2 } \right)\]

Answer 1

Hint: We will find the image of the given point after reflection about the line \[y = x\]. We will then find the coordinates of the point after the translation of the image along the \[x\] axis. We will use the formula for the rotation of a point about the origin to find the final position of the point.

Complete step-by-step answer:
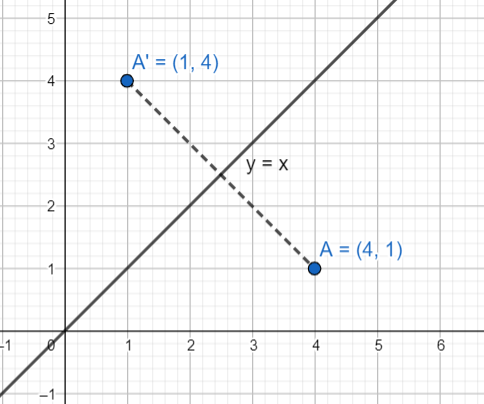
If any point (say \[\left( {a,b} \right)\]) is reflected about the line \[y = x\], then its image is the point \[\left( {b,a} \right)\]; that is the abscissa and the ordinate get interchanged.
So, the reflection of the point \[\left( {4,1} \right)\] about the line \[x = y\] will be the point \[\left( {1,4} \right)\].

Now, the point is translated through a distance of 2 units along the positive direction of the\[x\] axis.
So, the new point’s abscissa or the \[x\] coordinate will be 2 units more than the older abscissa. We will find the new point:
\[ \Rightarrow \left( {1 + 2,4} \right) = \left( {3,4} \right)\]

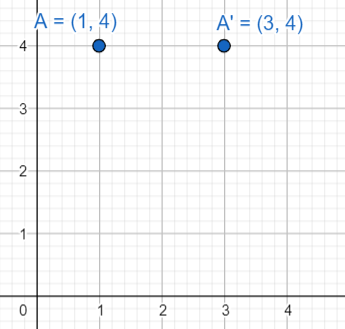
The new point will be \[\left( {3,4} \right)\].
Now, the point is rotated through an angle \[\dfrac{\pi }{4}\] about the origin in the anti-clockwise sense.

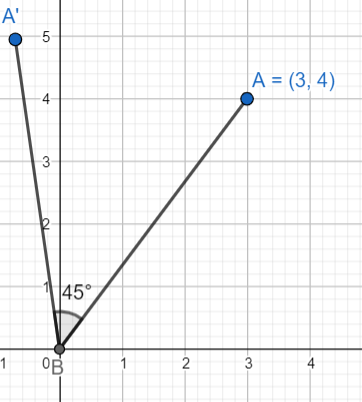
We will substitute \[45^\circ \] for \[\theta \], 3 for \[a\] and 4 for \[b\] in the formula for rotation of a point, \[\left( {a\cos \theta - b\sin \theta ,a\cos \theta + b\sin \theta } \right)\]. Therefore we get
\[\left( {a\cos \theta - b\sin \theta ,a\cos \theta + b\sin \theta } \right) = \left( {3\cos 45^\circ - 4\sin 45^\circ ,3\cos 45^\circ + 4\sin 45^\circ } \right)\]
Substituting the values of all trigonometric function, we get
\[\begin{array}{l} \Rightarrow \left( {3\cos 45^\circ - 4\sin 45^\circ ,3\cos 45^\circ + 4\sin 45^\circ } \right) = \left( {\dfrac{3}{{\sqrt 2 }} - \dfrac{4}{{\sqrt 2 }},\dfrac{3}{{\sqrt 2 }} + \dfrac{4}{{\sqrt 2 }}} \right)\\ \Rightarrow \left( {3\cos 45^\circ - 4\sin 45^\circ ,3\cos 45^\circ + 4\sin 45^\circ } \right) = \left( { - \dfrac{1}{{\sqrt 2 }},\dfrac{7}{{\sqrt 2 }}} \right)\end{array}\]
$\therefore $ The final position of the point is \[\left( { - \dfrac{1}{{\sqrt 2 }},\dfrac{7}{{\sqrt 2 }}} \right)\].
Option C is the correct option.

Note: If we get a case where the a point is rotated by an angle of \[\theta \] about the origin in the clockwise direction, we will substitute \[ - \theta \] in the formula instead of \[\theta \]. We can derive this formula using vector calculus and the Pythagoras theorem.
When a point (say \[\left( {a,b} \right)\]) is rotated by an angle \[\theta \] about the origin, then the coordinates of the new point are \[\left( {a\cos \theta - b\sin \theta ,a\cos \theta + b\sin \theta } \right)\].