Question

The point at which the gravitational force acting on any mass is zero due to the Earth and the Moon system is
(The mass of the Earth is approximately 81 times the mass of the Moon and the distance between the Earth and the Moon is 3,85,000 km.)
A. 36,000 km from the Moon
B. 38,500 km from the Moon
C. 34,500 km from the Moon
D. 30,000 km from the Moon

Answer 1

Hint:We need to equate the expressions for the gravitational force on a mass due to earth and moon respectively. Assuming a distance x of a certain mass from earth and solving the expression for the unknown parameter x, we can get the required answer.

Formula used:
The expression for gravitational force is given as
$F = G\dfrac{{{m_1}{m_2}}}{{{r^2}}}$

Complete answer:
Let the point at which the gravitational force acting on any mass is zero due to the Earth and the Moon system be at a distance x from the centre of earth. A mass m is at the distance x from the centre of earth. If total distance between centre of earth and moon is d then its value is given as
$d = 385000{\text{ }}km$

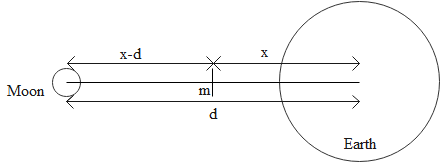
Let M be the mass of the moon then according to given information, the mass of earth is 81M.
The gravitational force on mass m due to earth is given as
${F_E} = G\dfrac{{81Mm}}{{{x^2}}}$
Here G is known as the gravitational constant.
Similarly, the gravitational force on mass m due to moon is given as
${F_M} = G\dfrac{{Mm}}{{{{\left( {d - x} \right)}^2}}}$
For the gravitational force to be zero for mass m, the forces due to earth and moon must be equal and being in opposite directions they cancel each other.
Therefore, we can write,
${F_E} = {F_M}$
Inserting the value of these expressions we get
$
  \Rightarrow G\dfrac{{81Mm}}{{{x^2}}} = G\dfrac{{Mm}}{{{{\left( {d - x} \right)}^2}}} \\
  \Rightarrow \dfrac{{81}}{{{x^2}}} = \dfrac{1}{{{{\left( {d - x} \right)}^2}}} \\
  \Rightarrow \dfrac{9}{x} = \dfrac{1}{{\left( {d - x} \right)}} \\
  \Rightarrow 9\left( {d - x} \right) = x \\
  \Rightarrow 9d - 9x = x \\
  \Rightarrow 10x = 9d \\
  \Rightarrow x = 0.9d \\
$
Substituting value of d we get,
$x = 346500km$
Distance from moon is
$d - x = 385000 - 346500 = 38500m$

So, the correct answer is “Option B”.

Note:
It should be noted that this point where gravitational force is zero is closer to the moon as compared to earth. This happens because the gravitational pull of earth is stronger than that of the moon due to which we need to go farther away from earth and closer to the moon in order to get this point where the two gravitational forces match and cancel each other.