Question

The point (-3,2) and (2,-3) lie in the
A.Same quadrant
B.II and III quadrant respectively.
C.II and IV quadrant respectively
D.IV and II quadrant respectively.

Answer 1

Hint: We need to find the corresponding quadrants for two points and the points are \[\left( -3,2 \right)\] and \[\left( 2,-3 \right)\] . We know that the quadrant II has negative coordinates of x and positive coordinates of y. Quadrant IV has positive values of x and negative values of y. So, follow this and decide about the quadrants of the points \[\left( -3,2 \right)\] and \[\left( 2,-3 \right)\] .

Complete step-by-step answer:

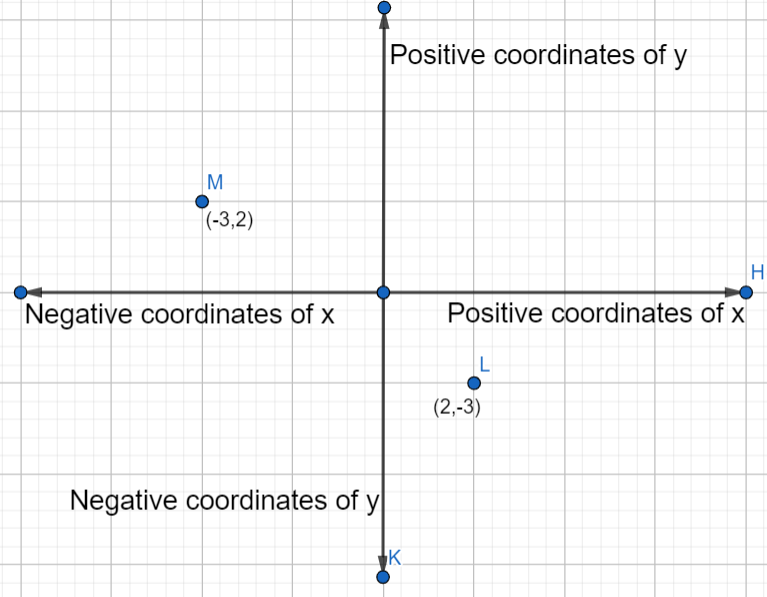
According to the question, we have two points given and the coordinates of the points are \[\left( -3,2 \right)\] and \[\left( 2,-3 \right)\] .
We know that the quadrant II has negative coordinates of x and positive coordinates of y. Quadrant IV has positive values of x and negative values of y.
Here, the point \[\left( -3,2 \right)\] has -3 as its x coordinates which is negative and 2 as its y coordinates which is positive. We know that quadrant II has negative values of x coordinates and positive values of y coordinates. So, the point \[\left( -3,2 \right)\] belongs to quadrant II.
The second point is \[\left( 2,-3 \right)\] , has 2 as its x coordinates which is positive and -3 as its y coordinates which is negative. We know that quadrant IV has positive values of x coordinates and negative values of y coordinates. So, the point \[\left( 2,-3 \right)\] belongs to quadrant IV.
So, \[\left( -3,2 \right)\] belongs to quadrant II and \[\left( 2,-3 \right)\] belongs to quadrant IV.
Hence, the correct option is option C.

Note: In this question, one might go with option B because quadrant III has negative coordinates of y and \[\left( 2,-3 \right)\] also has a negative coordinate of y. This approach is wrong. We should also think about the x coordinate of the point which is positive here and quadrant III doesn’t have a positive coordinate of x. So, option B is not correct.