Question

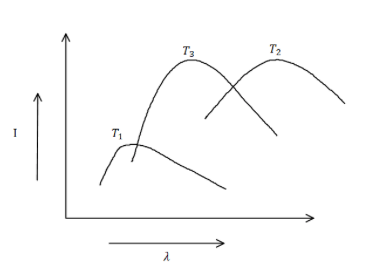
The plots of intensity versus wavelength for these three black bodies at temperatures ${T_1},{T_2}{\text{ and }}{T_3}$ respectively are shown in fig. Their temperatures are such that:

A) ${T_1} > {T_2} > {T_3}$.
B) ${T_1} > {T_3} > {T_2}$.
C) ${T_2} > {T_3} > {T_1}$.
D) ${T_3} > {T_2} > {T_1}$

Answer 1

Hint:Intensity is defined as the power of the wave per unit area. Black bodies are those bodies which behave as perfect absorbers and it does not have any reflecting power. The energy of the wave varies proportional to the temperature but is inversely proportional to the wavelength of the wave.

Formula used:The formula of the emissive power of wave is black body given by,
${E_b} = \sigma {T^4}$
Where energy from the black body is ${E_b}$ the Stefan-Boltzmann constant is $\sigma $ and the temperature is$T$.
The formula of the Wien’s law displacement is given by,
${\lambda _{\max .}} \cdot T = 2898$
Where maximum wavelength is ${\lambda _{\max .}}$ and temperature is T.

Complete step by step answer:
It is given that there are three black bodies and intensity versus wavelength is given and we need to arrange the temperature of the three bodies in ascending order.
From the diagram it is visible that,
\[ \Rightarrow {\lambda _2} > {\lambda _3} > {\lambda _1}\]………eq. (1)
The formula of the Wien’s law displacement is given by,
${\lambda _{\max .}} \cdot T = 2898$
Where maximum wavelength is ${\lambda _{\max .}}$and temperature is T.
$ \Rightarrow {\lambda _{\max .}} \cdot T = 2898$
$ \Rightarrow {\lambda _{\max .}} \cdot T = C$
Where C is constant.
$ \Rightarrow {\lambda _{\max .}} = \dfrac{C}{T}$
$ \Rightarrow {\lambda _{\max .}} \propto \dfrac{1}{T}$
Therefore the arrangement of the wavelength in equation (1) will be.
\[ \Rightarrow {\lambda _2} > {\lambda _3} > {\lambda _1}\]
Replace the values of the wavelength with the temperature and according to the relation of inversely proportional.
\[ \Rightarrow {T_1} > {T_3} > {T_2}\]
The arrangement of the temperature in ascending order is equal to\[{T_1} > {T_3} > {T_2}\].

The correct answer for this problem is option B

Note:It is advisable for students to remember the formula of the emissive power of the black bodies and also the formula of the Wien’s displacement as it can be helpful in problem solving. The unit of wavelength in the Wien’s displacement ($\mu m$) which is micrometer.