Question

The place(s) where the value of 'g' is unaffected by the increase (or) decrease in the speed of rotation of the earth about its own axis is-
(A) The north pole
(B) The south pole
(C) The equator
(D) None of the above

Answer 1

Hint
 We will use the parallelogram law of vectors to solve the equation. If two vectors are acting simultaneously at a point, then it can be represented both in magnitude and direction by the adjacent sides drawn from a point.

Complete step by step answer
According to the picture we can applied parallelogram law of vector addition,

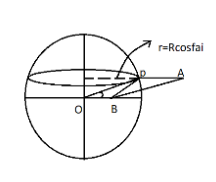
Now,$P{B^2} = P{O^2} + P{A^2} + 2POPAcos(180^\circ - \phi )$
Let us assume B is the point where the value of g is affected.
So,
$\Rightarrow {(m{g^1})^2} = {(mg)^2} + {(m{w^2}Rcos\phi )^2} + 2mgm{w^2}Rcos\phi ( - cos\phi ) $
$\Rightarrow {m^2}{g^1}^{^2} = {m^2}{g^2} + {m^2}{w^4}{R^2}co{s^2}\phi - 2{m^2}g{w^2}Rco{s^2}\phi $
$\therefore {g^{{1^2}}} = {g^2}(1 + \dfrac{{{w^4}{R^2}co{s^2}\phi }}{{{g^2}}} - \dfrac{{2{w^2}Rco{s^2}\phi }}{g})$
Here $w$ is very small.
So, $w^2$ can be neglected and the term containing $w^4$ can be neglected,
${g^{{1^2}}} = {g^2}(1 - \dfrac{{2{w^2}Rco{s^2}\phi }}{g})$
Or,${g^1} = g{(1 - \dfrac{{2{w^2}Rco{s^2}\phi }}{g})^{\dfrac{1}{2}}}$
Now, applying binomial expansion and neglecting higher powers we get,
$\;\therefore {g^1} = g(1 - \dfrac{1}{2} \times \dfrac{{2{w^2}Rco{s^2}\phi }}{g})$
$ \Rightarrow {g^1} = g(1 - \dfrac{{{w^2}Rco{s^2}\phi }}{g})$
$ \Rightarrow {g^1} = g - {w^2}Rco{s^2}\phi $
At poles,$\phi =90^0$
∴ $g^1 = g$ which is independent of $w$.
Thus the places where the value of ′$g$′ is unaffected by the increase/decrease in the speed of rotation of the earth about its own axis are the north and south poles.

Note
It actually depends upon exactly where on Earth you fall. $g$ is not truly constant; it varies from location to location. $9.8 m/s^2$ is just an average. The true value varies with your latitude and longitude (mainly due to surface variations in Earth's density).