
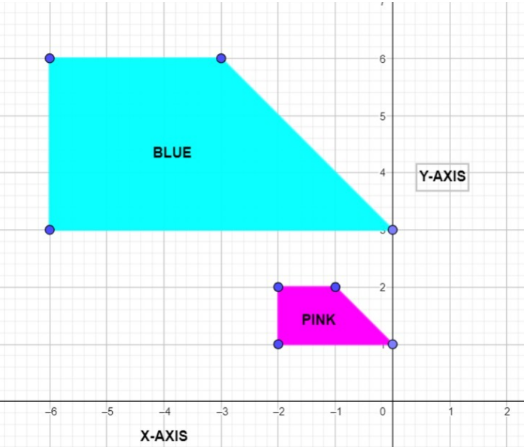
The pink trapezoid is dilated by a factor of $3$ . The resulting image is shown in blue. What is the ratio of the perimeters of the two trapezoids?

Answer
513.6k+ views
Hint: In order to solve the question, we need to understand the given mathematical statement properly. Dilation is a transformation which is used to make the objects or resize figures larger or smaller .The trapezoid is a type of quadrilateral having at least one pair of parallel sides which are opposite to each other. Perimeter of a shape is the total sum of length of the sides of the figure. To find the trapezoid’s perimeter we just sum up the lengths of all four sides. Also both the trapezoids are similar but have different side lengths as shown in the graph given.
Complete step by step answer:
In the given graph, we can see the two trapezoids which are not exactly same but similar.
We are given that the pink trapezoid is dilated by a factor of $3$. The resultant image is the trapezoid in blue. So, this means that the sides of the blue trapezoid are three times in length as compared to the sides of the pink trapezoid. So, all the sides of the blue trapezoid are triple the sides of the pink trapezoid in terms of length. If we assume the lengths of the sides of the pink trapezoid as w, x, y, and z.
Then, the length of the sides of the blue trapezium will be $3w$, $3x$, $3y$, and $3z$.Now, the perimeter of trapezoids can be calculated by adding up the side lengths. So, we get,
Perimeter of pink trapezoid$ = w + x + y + z$
Perimeter of blue trapezoid$ = 3w + 3x + 3y + 3z$
\[ = 3\left( {w + x + y + z} \right)\]
So, we can see that the perimeter of the blue trapezoid is three times the perimeter of the pink trapezoid. Hence,
$Perimeter\,of\,blue\,\,trapezoid = 3\left( {Perimeter\,of\,pink\,\,trapezoid} \right)$
Hence, the ratio of the perimeter of the blue trapezoid to the pink trapezoid is $3:1$.
Note:Always try to understand the mathematical statement carefully and keep things distinct .We must remember the properties of shapes and apply them appropriately. We must know the difference between the terms – ‘similar’ and ‘same’. Try to solve the question using the diagram which makes it visual and easy to understand. Cross check the answer and always keep the final answer simplified.
Complete step by step answer:
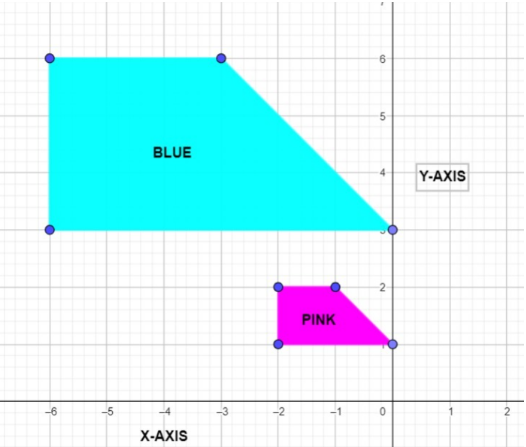
In the given graph, we can see the two trapezoids which are not exactly same but similar.

We are given that the pink trapezoid is dilated by a factor of $3$. The resultant image is the trapezoid in blue. So, this means that the sides of the blue trapezoid are three times in length as compared to the sides of the pink trapezoid. So, all the sides of the blue trapezoid are triple the sides of the pink trapezoid in terms of length. If we assume the lengths of the sides of the pink trapezoid as w, x, y, and z.
Then, the length of the sides of the blue trapezium will be $3w$, $3x$, $3y$, and $3z$.Now, the perimeter of trapezoids can be calculated by adding up the side lengths. So, we get,
Perimeter of pink trapezoid$ = w + x + y + z$
Perimeter of blue trapezoid$ = 3w + 3x + 3y + 3z$
\[ = 3\left( {w + x + y + z} \right)\]
So, we can see that the perimeter of the blue trapezoid is three times the perimeter of the pink trapezoid. Hence,
$Perimeter\,of\,blue\,\,trapezoid = 3\left( {Perimeter\,of\,pink\,\,trapezoid} \right)$
Hence, the ratio of the perimeter of the blue trapezoid to the pink trapezoid is $3:1$.
Note:Always try to understand the mathematical statement carefully and keep things distinct .We must remember the properties of shapes and apply them appropriately. We must know the difference between the terms – ‘similar’ and ‘same’. Try to solve the question using the diagram which makes it visual and easy to understand. Cross check the answer and always keep the final answer simplified.
Recently Updated Pages
Master Class 9 General Knowledge: Engaging Questions & Answers for Success

Master Class 9 Social Science: Engaging Questions & Answers for Success

Master Class 9 English: Engaging Questions & Answers for Success

Master Class 9 Maths: Engaging Questions & Answers for Success

Master Class 9 Science: Engaging Questions & Answers for Success

Class 9 Question and Answer - Your Ultimate Solutions Guide

Trending doubts
Difference Between Plant Cell and Animal Cell

Fill the blanks with the suitable prepositions 1 The class 9 english CBSE

Who is eligible for RTE class 9 social science CBSE

Which places in India experience sunrise first and class 9 social science CBSE

What is pollution? How many types of pollution? Define it

Name 10 Living and Non living things class 9 biology CBSE





