Question

The pilot of an aircraft flying horizontally at a speed $1200\,km\,{h^{ - 1}}$ . Observes that the angle of depression of a point on the ground changes from ${30^ \circ }$ to ${45^ \circ }$ in 15 sec. Find the height at which the aircraft is flying.

Answer 1

Hint: The question uses a concept of both trigonometry and motion in plane to yield the answer. Evaluate the question and understand the situation properly. Using relation between speed, distance and time; correct geometry and correct trigonometric expression will lead to the answer.

Complete answer:
Evaluating the problem gives a simplified overview as:

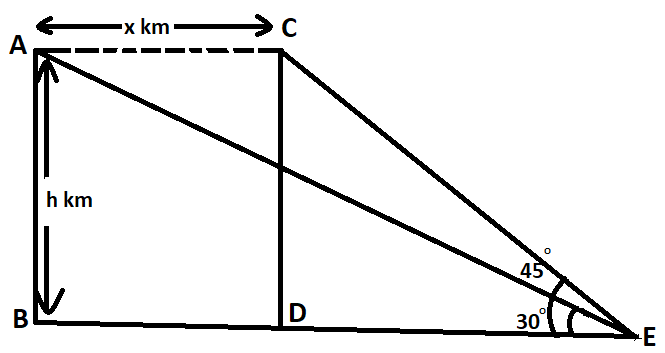
A and C are the initial and final points of observation by the pilot, AB and CD are the height above ground of the plane.
Initially with the speed and time provided to us we can calculate the horizontal distance covered by the plane in the provided time (denoted by x in diagram).
Distance (x) = Speed $ \times $ Time
Putting value of speed and time from question:
$x = 1200 \times \dfrac{{15}}{{3600}} = 5\,km$ ……… (i)
In the above step time is being converted into hours to balance the dimensions of units.
Assume height of plane from ground is h km,
In $\Delta CDE$
$\tan {45^ \circ } = 1 = \dfrac{{CD}}{{DE}} = \dfrac{h}{{DE}}$
From above equation it is evident that
DE = h ……… (ii)
Now in $\Delta ABE$ ,
$\tan {30^ \circ } = \dfrac{1}{{\sqrt 3 }} = \dfrac{{AB}}{{BE}} = \dfrac{h}{{DE + x}}$
Evaluating above problem by putting values of x and DE from the equation (i) and (ii) respectively will yield,
$\dfrac{1}{{\sqrt 3 }} = \dfrac{h}{{h + 5}}$
Solving above equation to get value of h will give,
$h = 6.83\,km$
Plane is flying at a height $h = 6.83\,km$ above the ground.

Note:
Very often we forget to replace every unit to the same dimensions and lead to wrong answers, which is to be surely avoided. Kinematics deals with motion of objects with factors like velocity, distance, time and acceleration. Certain factors that are neglected include air resistance.