Question

The picture below shows that roller coaster on a track where friction is negligible. What is the ranking of the speeds at the indicated locations from highest speed to lowest speed? Assume that the roller coaster has enough speed at the beginning to make it through the entire trip.

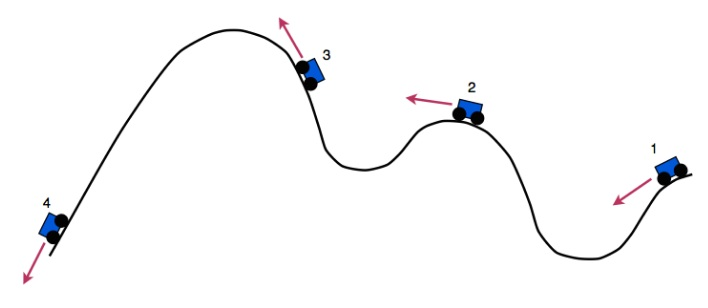
(A) $ 1,2,3,4 $
(B) $ 4,3,2,1 $
(C) $ 3,2,1,4 $
(D) $ 4,1,2,3 $
(E) $ 2,1,3,4 $

Answer 1

Hint :Here, we have been given the figure of a roller coaster where it has been shown the different positions of the roller coaster. So, we have to use the conservation of energy concept to know where the velocity of a roller coaster will be higher as well as lower.

Complete Step By Step Answer:
Here, the roller coaster is moving on the smooth surface and with no friction between them. Now, we are going to use the law of conservation of energy as:
 $ P.E. + K.E. = $ Constant
The energies will be constant, let $ k $ be the constant in the above equation. Thus the above equation is given by:
 $ P.E. + K.E. = k $
 $ \Rightarrow mgh + \dfrac{1}{2}m{v^2} = k $
 $ \Rightarrow v = \sqrt {\dfrac{2}{m}(k - mgh)} $
So, the above relation between speed and the height in the above equation is obtained. The speed of the roller coaster depends on the height of the roller coaster.
The speed is higher when it is at the lowest point of the surface is shown by the relation between speed and height.
Thus, the speed of the roller coaster is higher at point $ 4 $ and lowest at point $ 3 $ in the above figure.
The required answer is option D.

Note :
Here, we have observed that the speed of the rollercoaster is high when the coaster is at lowest height. This can be understood when we derive the relation between the velocity and the height. And we have obtained the answer.