Question

The period of simple pendulum is doubled, when
A.The length is doubled
B.The mass of the bob is doubled
C.Its length is made four times
D.The mass of the bob and the length of the pendulum are doubled the period

Answer 1

Hint: A simple pendulum performs periodic motion along its axis, in which a small bob of mass m is attached to a string of length L. To solve the above problem we will discuss the dependencies of the time period of a simple pendulum on different factors and by varying one of these factors we will calculate our required answer.

Formula used:
Time period
$\Rightarrow T=2\pi \sqrt{\dfrac{L}{g}}$

Complete answer:
Oscillatory motion can be defined as to or fro motion of an object in a periodic fashion along an equilibrium position by taking time T for one complete oscillation known as time period.
The maximum distance travelled from the equilibrium position is known as the amplitude of that oscillatory motion.

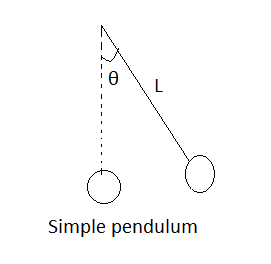
The motion of a simple pendulum is a periodic motion in which the bob of a pendulum is oscillating about the mean position within a particular time period.
Now, time period of simple pendulum is given by
$\Rightarrow T=2\pi \sqrt{\dfrac{L}{g}}....(1)$
Here, we can observe that the time period is independent of mass of the bob of the pendulum and assuming g constant at particular position, the only varying quantity is length of pendulum.
Let us assume the initial length of pendulum be L so the time period will be T, now the new length is ${{L}^{'}}$ and the time period is 2T, so
$\Rightarrow 2T=2\pi \sqrt{\dfrac{{{L}^{'}}}{g}}.....(2)$
By dividing equation (2) by (1) we have,
$\Rightarrow \dfrac{2T}{T}=\dfrac{2\pi \sqrt{\dfrac{{{L}^{'}}}{g}}}{2\pi \sqrt{\dfrac{L}{g}}}$
$\Rightarrow \sqrt{\dfrac{{{L}^{'}}}{L}}=2$
Squaring both sides we have,
$\Rightarrow \dfrac{{{L}^{'}}}{L}=4$
$\Rightarrow {{L}^{'}}=4L$
$\therefore $ By increasing the length of a simple pendulum by four times the time period will be doubled.

Hence, option (C) is correct.

Note:
Simple harmonic motions are special cases of oscillatory motion as all simple harmonic motions are oscillatory as well as periodic but not all oscillatory motions are not simple harmonic. Simple harmonic motions can be of two types, 1) Linear SHM in which the restoring force acting on a particle is directly proportional to its displacement. 2) Angular SHM in which the system oscillates angular along a fixed axis.