Question

The period of oscillation of a simple pendulum of length L suspended from the roof of a rocket acceleration upwards with a constant acceleration (g) is given by?
(A) Infinity
(B) Zero
(C) $2\pi \sqrt {\dfrac{L}{{2g}}} $
(D) $2\pi \sqrt {\dfrac{L}{g}} $

Answer 1

Hint: First we need to draw a free body diagram representing all the parameters required to solve this problem. Now by taking the rocket as the frame of reference we can find the effective acceleration acting on the pendulum which is acting downward. Now applying the time period formula we can find the solution to this problem.

Complete step by step answer:
As per the problem we know that a simple pendulum of length L suspended from the roof of a rocket accelerates upwards with a constant acceleration (g).
Now we need to find the time period of the simple pendulum.

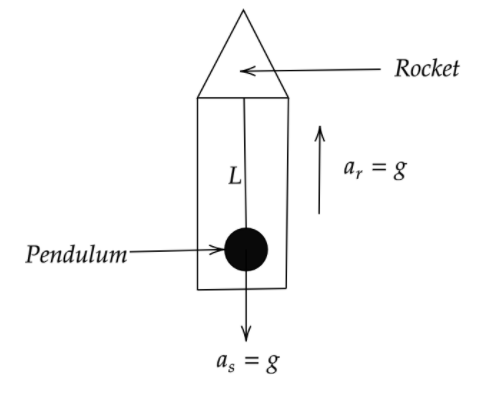
Here in this problem the rocket accelerates with a constant acceleration of g in the upward direction. From the figure we can say that a rocket is an acceleration frame of reference. As we know that Newton's law is not applicable in the acceleration frame of reference hence if we want to use Newton's law of motion in the acceleration frame of reference then we have to use a pseudo acceleration that is acting on the pendulum.
Since the rocket is accelerating in an upward direction same as that of the acceleration due to gravity and the pendulum bob experiences downward pseudo acceleration which is also equal to g.
Therefore the effective acceleration acting on the pendulum is equals to,
${a_{eff}} = {a_r} - {a_s}$
Where,
${a_{eff}}$ is the effective acceleration of the pendulum.
${a_r}$ is the acceleration due to the frame of reference that is g.
And ${a_s}$ is the pseudo acceleration that is –g.
Now putting the respective values we will get,
${a_{eff}} = g - \left( { - g} \right) = 2g$
We know the periodic time of a simple pendulum as,
$T = 2\pi \sqrt {\dfrac{L}{{{a_{eff}}}}} $
$ \Rightarrow T = 2\pi \sqrt {\dfrac{L}{{2g}}} $
Therefore the correct option is (C).

Note: Remember that here the pseudo force acting on the pendulum is opposite to the direction of acceleration of the frame of reference and the pseudo force or acceleration is always equal to the magnitude of the reference acceleration or force. Note that pseudo force or acceleration is an apparent force that acts on all the masses whose motion is described using a non-inertial frame of reference.