Question

The perimeter of rhombus is 40 cm and length of one of its diagonal is 12 cm then area of rhombus is
A.95 $cm^2$
B.96 $cm^2$
C.97 $cm^2$
D.98 $cm^2$

Answer 1

Hint: A rhombus is a quadrilateral with all equal sides and opposite sides is parallel to each other. In rhombus diagonals bisect each other at 90o.
Formula used :- area of rhombus \[ = \,\dfrac{{product\,of\,diagonals}}{2}\,\, = \,\dfrac{{{d_1}\, \times \,{d_2}}}{2}\]

Complete step-by-step answer:
Given,
Perimeter of rhombus is 40 cm
Length of one diagonal is 12 cm
We know that
Perimeter of rhombus = $4\, \times \,side$
Therefore we will find side of rhombus firstly using formula of perimeter and given perimeter
$
  40\,cm\, = \,4\, \times \,side \\
  \dfrac{{40\,cm}}{4}\, = \,side \\
  10\,cm\, = \,side \\
$

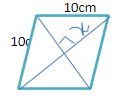
we have to find area of rhombus that requires another diagonal also
let’s find another diagonal
using Pythagoras theorem
$H^2$ = $P^2$ +$B^2$
$
  {10^2}\, = \,{6^2}\, + \,{x^2} \\
\Rightarrow 100\, = \,36\, + \,{x^2} \\
 \Rightarrow 100 - 36\, = {x^2} \\
\Rightarrow 64\, = \,{x^2} \\
\Rightarrow \sqrt {64\,\,} \, = \,x \\
\Rightarrow 8\, = \,x \\
$
So our diagonal will be (8 +8 )cm = 16 cm
Finally we will find area of rhombus with the help of our diagonals
$
  area\, = \dfrac{{{d_1}\, \times \,{d_2}}}{2}\, \\
 \Rightarrow area\,\, = \,\dfrac{{12 \times 16}}{2} \\
\Rightarrow area\, = \,6\, \times \,16\,c{m^2} \\
\Rightarrow area\, = \,96\,c{m^2} \\
$
Therefore the area of rhombus is 96 $cm^2$.
Hence the correct option is (B).

Note: Rhombus is a special case of quadrilateral and all sides are equal but we cannot simply find its area by using the area of square = side × side .
It has its formula which is a product of diagonals divided by two.
We can also find area of rhombus using area of triangle $ = \,\dfrac{1}{2}\, \times \,b\, \times \,h$
Simply dividing rhombus in two triangles
Area of rhombus = area of first triangle + area of second triangle
Moreover, go for the easiest process and proceed with the values required.