Question

The perimeter of an isosceles triangle is equal to 14cm. The ratio of the lateral side to the base is 5:4. The area of the triangle is
[a] $\dfrac{1}{2}\sqrt{21}c{{m}^{2}}$
[b] $\dfrac{3}{2}\sqrt{21}c{{m}^{2}}$
[c] $\sqrt{21}c{{m}^{2}}$
[d] $2\sqrt{21}c{{m}^{2}}$

Answer 1

Hint: Assume that the base is of length x centimetres. Use the fact that the ratio of the lateral side to the base is 5:4 to find the length of the lateral side in terms of x. Use the fact that the perimeter of a triangle is the sum of its sides and hence find the perimeter of the triangle in terms of x. Equate this expression to 14 and hence find the value of x and hence the length of the sides of the triangle. Use heron's formula, i.e. $\Delta =\sqrt{s\left( s-a \right)\left( s-b \right)\left( s-c \right)}$, where the symbols have their usual meanings to find the area of the triangle.

Complete step by step solution:

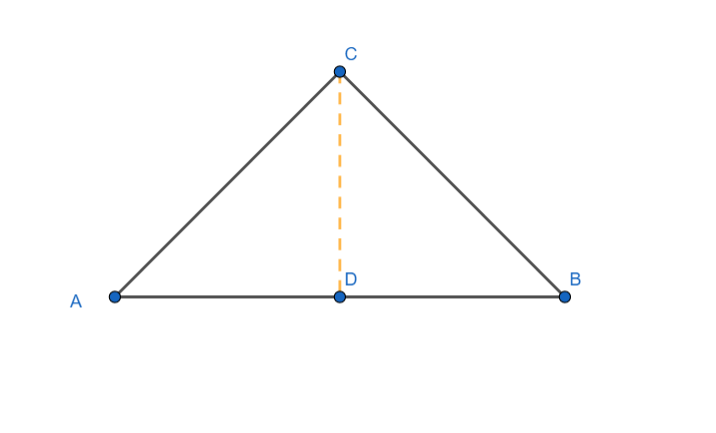
Given: ABC is an isosceles triangle with AC = BC. The perimeter of the triangle is 14cm and AC: AB = 5:4
To determine: Area of the triangle ABC.
Construction: Draw CD perpendicular to AB
Let AB = x centimeters.
Now, we have
AC:AB = 5:4.
Since in a proportion product of means is equal to the product of extremes, we have
4AC = 5AB
Hence, we have
4AC = 5x
Dividing both sides by 4, we get
$AC=\dfrac{5}{4}x$
Now, we have the perimeter of ABC= AB+BC+AC $=x+\dfrac{5x}{4}+\dfrac{5x}{4}=\dfrac{4x+5x+5x}{4}=\dfrac{7x}{2}$
But given that the perimeter is 14cm.
Hence, we have
$\dfrac{7x}{2}=14$
Multiplying by 2 on both sides, we get
7x= 28
Dividing by 7 on both sides, we get
x = 4cm.
Hence the length of the base AB = 4cm.
Hence, we have
$AC=BC=\dfrac{5x}{4}=5cm$
Since ABC is an isosceles triangle with AC = BC and CD is the altitude on the base, we have AD = BD
Hence, we have
AD = 2cm.
We know that in a right-angled triangle, the square of the hypotenuse is equal to the sum of the squares of the other sides.
Hence, in triangle ADC, we have
$A{{D}^{2}}+D{{C}^{2}}=A{{C}^{2}}$
Substituting DC = 2 and AC = 5, we get
$C{{D}^{2}}+4=25$
Subtracting 4 on both sides, we get
$C{{D}^{2}}=21$
Hence, we have
$CD=\sqrt{21}$
We know that the area of a triangle is equal to half the product of base and height.
Hence, we have
$ar\left( \Delta ABC \right)=\dfrac{1}{2}CD\times AB=\dfrac{1}{2}\times \sqrt{21}\times 4=2\sqrt{21}$ square centimetres.
Hence option [d] is correct.
Note: Alternative solution: Using heron's formula:
We can also find the area using heron’ s formula.
Here, in triangle ABC, we have
a = 5cm, b = 5cm and c = 4cm
Hence, we have
$s=\dfrac{a+b+c}{2}=\dfrac{5+5+4}{2}=7$
We know by heron's formula
$\Delta =\sqrt{s\left( s-a \right)\left( s-b \right)\left( s-c \right)}$
Hence, we have
$ar\left( \Delta ABC \right)=\sqrt{7\left( 7-5 \right)\left( 7-5 \right)\left( 7-3 \right)}=2\sqrt{21}$, which is the same as obtained above
Hence option [d] is correct.