Question

The perimeter of an equilateral triangle is $32$ centimetres. How do you find the length of an altitude of the triangle?

Answer 1

Hint: Since the triangle in the above question is given to be equilateral, we can assume the length of the each of its three sides to be equal to $a$ centimetres so that its total perimeter will become equal to $3a$ centimetres. According to the question, the perimeter is equal to $32$ centimetres so we will be able to write the equation $3a=32$ from which the side of the triangle can be evaluated. For finding out the length of an altitude, we need to drop a perpendicular from a vertex onto the opposite side and then using trigonometry, we can determine the required length.

Complete step-by-step answer:
According to the question, the triangle is an equilateral triangle. Therefore, let us assume the length of each of the three sides of this triangle to be equal to $a$ centimetres. Therefore, the triangle can be represented as in the below figure.

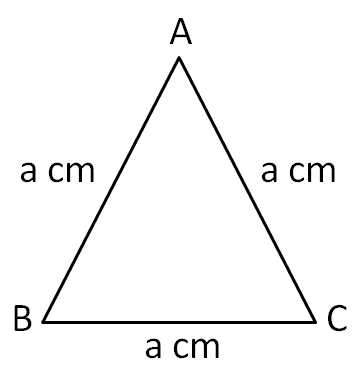
From the above figure, we can write the perimeter of the triangle as
$\begin{align}
  & \Rightarrow P=AB+BC+AC \\
 & \Rightarrow P=a+a+a \\
 & \Rightarrow P=3a \\
\end{align}$
Now, since according to the question the perimeter of the triangle is given to be equal to $32$ centimetres, we can write
$\Rightarrow P=32$
From the above two equations, we can write
$\Rightarrow 3a=32$
Dividing both the sides by $3$, we will get
$\begin{align}
  & \Rightarrow \dfrac{3a}{3}=\dfrac{32}{3} \\
 & \Rightarrow a=\dfrac{32}{3}cm........\left( i \right) \\
\end{align}$
So the side of each side of the triangle is equal to $\dfrac{32}{3}$ centimeters. Now, we also know that the each angle of an equilateral triangle is equal to ${{60}^{\circ }}$. Therefore, the triangle can be drawn as

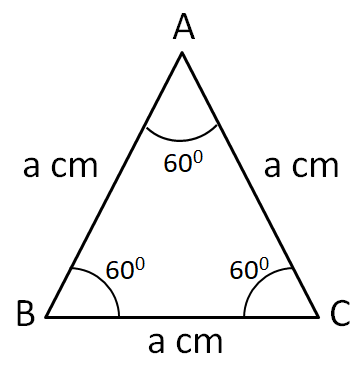
For determining the length of the altitude, we drop a perpendicular from A onto the side BC of the above triangle as shown below.

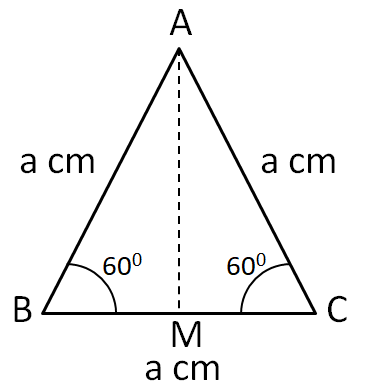
Now, we know that the altitude through a vertex in an equilateral triangle is also a bisector of the opposite side. Therefore, we can write $BM=\dfrac{a}{2}$. Now, from the triangle ABM we can write
\[\begin{align}
  & \Rightarrow \tan {{60}^{\circ }}=\dfrac{AM}{BM} \\
 & \Rightarrow \tan {{60}^{\circ }}=\dfrac{AM}{\dfrac{a}{2}} \\
 & \Rightarrow \tan {{60}^{\circ }}=\dfrac{2AM}{a} \\
\end{align}\]
Now, we know that $\tan {{60}^{\circ }}=\dfrac{\sqrt{3}}{2}$. Therefore, we will get
$\begin{align}
  & \Rightarrow \dfrac{\sqrt{3}}{2}=\dfrac{2AM}{a} \\
 & \Rightarrow AM=\dfrac{\sqrt{3}}{2}\times \dfrac{a}{2} \\
 & \Rightarrow AM=\dfrac{\sqrt{3}a}{4} \\
\end{align}$
From the equation (i) we can write
$\begin{align}
  & \Rightarrow AM=\dfrac{\sqrt{3}}{4}\times \dfrac{32}{3} \\
 & \Rightarrow AM=\dfrac{8}{\sqrt{3}}cm \\
\end{align}$
Hence, the length of the altitude is equal to $\dfrac{8}{\sqrt{3}}cm$.

Note: For solving these types of questions, we must have a good command over the concepts of the application of trigonometry. If we are not comfortable with trigonometry, we can also remember the length of the altitude of an equilateral triangle, which is found to be equal to $\dfrac{\sqrt{3}a}{4}$, where $a$ is the side of the equilateral triangle.