Question

The perimeter of a triangular field is 240 dm. If two of its sides are 50 dm and 78 dm, find the lengths of the perpendicular on the sides of length 50 dm from the opposite vertex to the nearest integer.

Answer 1

Hint: Here in this question, we need to find the height or length of the perpendicular on the sides of length 50 dm. For this, first we need to find the length of the third side of a triangle then find the area by using a Heron’s formula and further find the length by using a general formula of the area of the triangle by taking a base of length 50 dm. On further simplification we get the required solution.

Complete step-by-step solution:
The area of a triangle is defined as the total region that is enclosed by the three sides of any particular triangle. Basically, it is equal to half of the base times height, i.e.,
$$Area = \dfrac{1}{2} \times base \times height$$ or $$A = \dfrac{1}{2} \times b \times h$$. Hence, to find the area of a tri-sided polygon, we have to know the base (b) and height (h) of it.
Consider the given question:

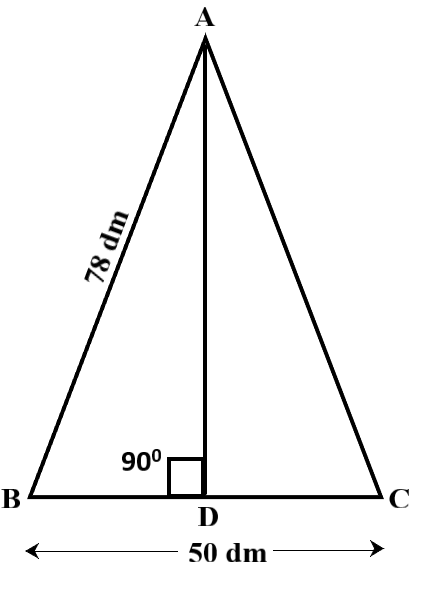
Given the perimeter of the triangle $$\vartriangle \,ABC$$ = 240 dm.
Length of two sides of triangle = 78 dm and 50 dm.
Length of third side of triangle $$ = 240 - \left( {78 + 50} \right)$$
$$ \Rightarrow \,\,240\,dm - 128\,dm$$
$$ \Rightarrow \,\,112\,dm$$
Now, find the area of triangle $$\vartriangle \,ABC$$ by using a Heron’s formula
i.e., $$Area = \sqrt {s\left( {s - a} \right)\left( {s - b} \right)\left( {s - c} \right)} $$
where, s is semi perimeter $$s = \dfrac{{a + b + c}}{2}$$
‘a’, ‘b’ and ‘c’ length sides of a triangle.
$$s = \dfrac{{112 + 78 + 50}}{2} = 120\,dm$$
$$ \Rightarrow \,\,Area = \sqrt {120\left( {120 - 50} \right)\left( {120 - 78} \right)\left( {120 - 112} \right)} $$
$$ \Rightarrow \,\,Area = \sqrt {120 \times 70 \times 42 \times 8} $$
$$ \Rightarrow \,\,Area = \sqrt {2822400} $$
$$ \Rightarrow \,\,Area = 1680\,sqdm$$
Now, to find the lengths of the perpendicular on the sides of length 50 dm.
Consider a formula of area of triangle
$$ \Rightarrow \,\,\,Area = \dfrac{1}{2} \times base \times height$$
$$ \Rightarrow \,\,\,height = 2 \times \dfrac{{Area}}{{base}}$$
$$ \Rightarrow \,\,\,height = 2 \times \dfrac{{1680}}{{50}}$$
$$ \Rightarrow \,\,\,height = \dfrac{{336}}{5}$$
$$\therefore \,\,\,height = 67.2\,dm$$
Hence, the length of the perpendicular on the sides of length 50 dm is 67.2 dm

Note: While determining the area we use the formula. The formula is $$A = \dfrac{1}{2} \times b \times h$$. The unit for the perimeter will be the same as the unit of the length of a side or triangle. Whereas the unit for the area will be the square of the unit of the length of a triangle. We should not forget to write the unit.