Question

The perimeter of a triangle ABC is 37cm and the ratio between the lengths of its altitudes be 6:5:4. Find the smallest length of its sides.

Answer 1

Hint: Here, first of all, let the sides of the triangle be x, y and z. Now, the perimeter is given so form an equation by adding x, y and z. Now, multiply the ratio with a and then separate the ratio for each individual altitude. Now, the area of triangle is given by
 $ \Rightarrow $ Area of $ \Delta = \dfrac{1}{2} \times b \times h $
Now, use all three sides and three altitudes to form an equation. Solve that equation and we will get the sides of the triangle.

Complete step-by-step answer:
In this question, we are given a triangle and its perimeter and the ratio of its altitudes. We need to find the smallest side of this triangle.
Let us draw the figure of this triangle.

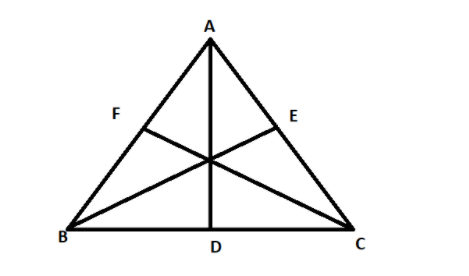
Here, we can see that $ \Delta ABC $ has three sides AB, BC and AC and three altitudes AD, BE and CF.
Let the sides of the triangle be x, y and z, that is $ AB = x,BC = y $ and $ AC = z $ . Now, the perimeter of the triangle is 37. Therefore, we get
 $ \Rightarrow x + y + z = 37 $ - - - - - - - - - - (1)
Now, the ratio of the lengths of altitude is 6:5:4. So, we can multiply this ratio with a and write
 $ \Rightarrow 6:5:4 = 6a:5a:4a $
So, we get $ AD = 6a,CF = 5a $ and $ BE = 4a $
Now, we know that the area of triangle is given by the formula
 $ \Rightarrow $ Area of $ \Delta = \dfrac{1}{2} \times b \times h $
Here, we have 3 sides and 3 altitudes, so we get
 $
   \Rightarrow \dfrac{1}{2} \times y \times 6a = \dfrac{1}{2} \times z \times 4a = \dfrac{1}{2} \times x \times 5a \\
   \Rightarrow 6y = 4z = 5x \;
  $
Therefore, we get
 $
   \Rightarrow 6y = 5x \\
   \Rightarrow y = \dfrac{{5x}}{6} \\
  $ and $
   \Rightarrow 4z = 5x \\
   \Rightarrow z = \dfrac{{5x}}{4} \;
  $
Putting these values in equation (1), we get
 $
   \Rightarrow x + y + z = 37 \\
   \Rightarrow x + \dfrac{{5x}}{6} + \dfrac{{5x}}{4} = 37 \\
   \Rightarrow \dfrac{{12x + 10x + 15x}}{{12}} = 37 \\
   \Rightarrow 37x = 12 \times 37 \\
   \Rightarrow x = 12 \;
  $
Therefore,
 $ \Rightarrow y = \dfrac{{5x}}{6} = \dfrac{{5\left( {12} \right)}}{6} = 10 $ and
 $ \Rightarrow z = \dfrac{{5x}}{4} = \dfrac{{5\left( {12} \right)}}{4} = 15 $
Hence, the lengths of sides of the triangle are 12cm, 10cm and 15cm.
Hence, the shortest side of triangle ABC will be $ BC = 10cm $ .
So, the correct answer is “10 cm”.

Note: For obtuse angled triangles altitude is drawn outside the triangle by extending the base till the foot of the altitude.
The altitude of an equilateral triangle bisects its base and the opposite angle.
The altitude of a right angled triangle divides the given triangle into two similar triangles.