Question

The perimeter of a sector of a circle of radius 5.2 cm is 16.4 cm. The area of the sector is:
(a) $15.1\text{ c}{{\text{m}}^{2}}$
(b) $15.5\text{ c}{{\text{m}}^{2}}$
(c) $15.6\text{ c}{{\text{m}}^{2}}$
(d) $15.9\text{ c}{{\text{m}}^{2}}$

Answer 1

Hint: We have a well-established formula for perimeter and area of sector of circle involving radius of circle which is given. So, by using those formulas we can easily solve our problem.

Complete step-by-step answer:
One of the most important branches of mathematics is geometry. It includes the analysis of figures using simple theorems and results. Perimeter can be defined as the total length of the boundary of a geometrical figure. Area can be defined as the space occupied by a flat shape or the surface of an object.

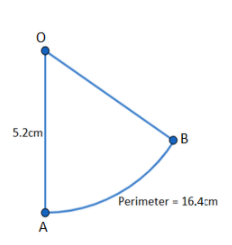
According to this problem, we are given that the perimeter of a sector of a circle of radius 5.2 cm is 16.4 cm. Let us consider a sector AOB with centre as O. The perimeter of this sector AOB is defined as the sum of arc length and two times radius of the sector. Therefore, mathematically it can be stated as:
\[\begin{align}
  & Perimeter=OA+OB+AB \\
 & Perimeter=r+r+arc\text{ }length \\
 & 16.4=5.2+5.2+arc\text{ }length \\
 & arc\text{ }length=6cm \\
\end{align}\]
Area of the sector = $\dfrac{1}{2}\times radius\times arc\text{ }length$.
Now, putting the values in the above problem,
$\begin{align}
  & A=\dfrac{1}{2}\times 5.2\times 6 \\
 & A=15.6\text{ c}{{\text{m}}^{2}} \\
\end{align}$
Therefore, the area of the sector is $15.6\text{ c}{{\text{m}}^{2}}$.
Hence, option (c) is correct.

Note: The key step for solving this problem is the knowledge of perimeter and area of the sector of a circle. By using the appropriate formula for sector of a circle, we evaluate the area of sector. Hence, the chances of error occurrence are minimized for better accuracy.