Question

The perimeter of a sector is constant. If its area is to be maximum, then the sectorial angle is
A. $\dfrac{\pi}{2}$
B.$ \dfrac{\pi}{4} $
C.$4^c$
D.$2^c$

Answer 1

Hint: Firstly, we will let the radius be $r$ and sectorial angle be $\theta $ . Given that, the perimeter of the sector is constant. Substitute the value of radius in the formula of area of the sector. Then, differentiate both sides with respect to $\theta $ . As the area is maximum so, we will put the differential value equal to zero and obtain the value of $\theta $. If the differentiated value is negative, then the area is maximum and the value of $\theta $ is correct otherwise not.

Complete step-by-step answer:
Let that the radius of the circle is $r$ and the sectorial angle be $\theta $ .
We draw a figure,
      

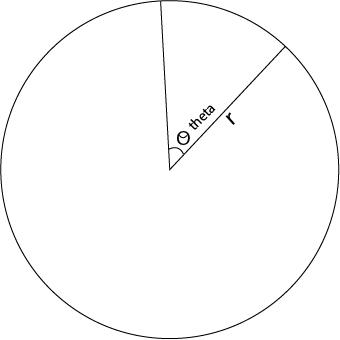
Now, the perimeter of the sector is given by $2r + r\theta $ , according to the question, the perimeter of the sector is constant.
 $2r + r\theta = k$
We will evaluate the value of $r$ ,
 $ \Rightarrow r = \dfrac{k}{{2 + \theta }}$
The area of sector is denoted by A and given by
 $A = \dfrac{1}{2}{r^2}\theta $
Now, substitute the value of radius of the above formula of area,
We get,
$A = \dfrac{{{k^2}}}{2} \times \dfrac{\theta }{{{{(\theta + 2)}^2}}}$
     We will differentiate the area on both side with respect to $\theta $ using the formula,
 $\dfrac{{d\left( {\dfrac{u}{v}} \right)}}{{dx}} = \dfrac{{v\left( {\dfrac{{du}}{{dx}}} \right) - u\left( {\dfrac{{dv}}{{dx}}} \right)}}{{{v^2}}}$
We get,
 $\
   \Rightarrow \dfrac{{dA}}{{d\theta }} = \dfrac{{{k^2}}}{2}\left\{ {\dfrac{{{{(\theta + 2)}^2} - 2\theta (\theta + 2)}}{{{{(\theta + 2)}^4}}}} \right\} \\
   \Rightarrow \dfrac{{dA}}{{d\theta }} = \dfrac{{{k^2}}}{2}\left( {\dfrac{{(\theta + 2)(\theta + 2 - 2\theta )}}{{{{(\theta + 2)}^4}}}} \right) \\
   \Rightarrow \dfrac{{dA}}{{d\theta }} = \dfrac{{{k^2}}}{2}\left( {\dfrac{{2 - \theta }}{{{{(\theta + 2)}^3}}}} \right)...........eq(1) \\
\ $
The area has to be maximum so, we will put the value of $\dfrac{{dA}}{{d\theta }}$ written as equation (1) equal to zero.
We get,
$\
\Rightarrow \dfrac{{dA}}{{d\theta }} = 0 \\
\Rightarrow \dfrac{{{k^2}}}{2}\left( {\dfrac{{2 - \theta }}{{{{(\theta + 2)}^3}}}} \right) = 0 \\
\Rightarrow 2 - \theta = 0 \\
\Rightarrow \theta = 2 \\
\ $
Again differentiate the equation (1) with respect to $\theta $ , we get,
 $\
   \Rightarrow \dfrac{{{d^2}A}}{{d{\theta ^2}}} = \dfrac{{{k^2}}}{2}\left[ {\dfrac{{2( - 3)}}{{{{(\theta - 2)}^4}}} - \dfrac{{{{(\theta + 2)}^3} \times 1 - \theta \times 3{{(\theta + 2)}^2}}}{{{{\left[ {{{\left( {\theta + 2} \right)}^3}} \right]}^2}}}} \right] \\
   \Rightarrow \dfrac{{{d^2}A}}{{d{\theta ^2}}} = \dfrac{{{k^2}}}{2}\left[ {\dfrac{{ - 6}}{{{{(\theta + 2)}^4}}} - \dfrac{{\theta + 2 - 3\theta }}{{{{(\theta + 2)}^4}}}} \right] \\
   \Rightarrow \dfrac{{{d^2}A}}{{d{\theta ^2}}} = \dfrac{{ - {k^2}}}{2}\left[ {\dfrac{6}{{{{(\theta + 2)}^4}}} + \dfrac{{2 - \theta }}{{{{\left( {\theta + 2} \right)}^4}}}} \right] \\
\ $
   Now, we will substitute the value of $\theta = 2$
We have,
$\
   \Rightarrow \dfrac{{{d^2}A}}{{d{\theta ^2}}} = \dfrac{{ - {k^2}}}{2}\left[ {\dfrac{6}{{{{(2 + 2)}^4}}} + \dfrac{{2 - 2}}{{{{(2 + 2)}^4}}}} \right] \\
   \Rightarrow \dfrac{{{d^2}A}}{{d{\theta ^2}}} = \dfrac{{ - {k^2}}}{2}\left[ {\dfrac{6}{{{{(4)}^4}}} + 0} \right] \\
   \Rightarrow \dfrac{{{d^2}A}}{{d{\theta ^2}}} = \dfrac{{ - 3{k^2}}}{{256}} \\
   \Rightarrow \dfrac{{{d^2}A}}{{d{\theta ^2}}} \prec 0 \\
\ $
We can conclude that the area is maximum as the double derivative of the area is negative at $\theta = {2^C}$ .
Hence, option (D) is correct.

Note: When we remember that the area is maximum when the double derivative is negative and minimum when the double derivative is positive.
We need to find the value of $\theta $ to determine that the double derivative is negative or positive. we have to remember the formula of area and the perimeter of the sector.