Question

The perimeter of a sector is a constant. If its area is to be maximum , then the sectorial angle is
A. $\dfrac{{{\pi }^{c}}}{6}$
B. $\dfrac{{{\pi }^{c}}}{4}$
C. ${{4}^{c}}$
D. ${{2}^{c}}$

Answer 1

Hint: To solve the above question first we will know the definition of sector or circle sector. A circle sector is the portion of a disk which is enclosed by two radii and an arc.

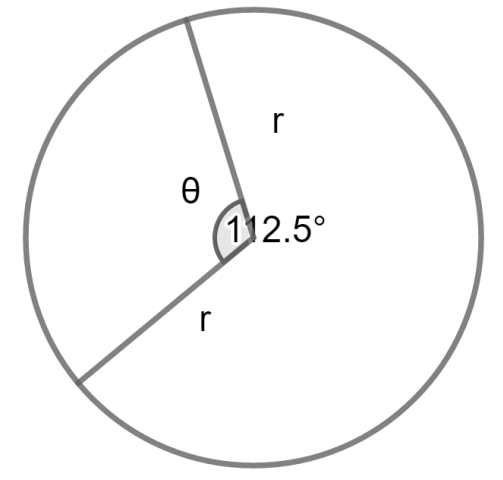
In the diagram, $\theta $ is the central angle, r is the radius of the circle. If $\theta $is measured in radians, then, area of sector = $\dfrac{1}{2}{{r}^{2}}\theta $ and the perimeter of the sector is $2r+r\theta $

Complete step by step solution:
Let r be the radius of the circle and $\theta $ be the sectorial angle of a sector of it. Then the perimeter of the sector is :
$\Rightarrow 2r+r\theta =k$
Where, k is the constant which is given in the question.
By above equation we will find the radius of the circle as:
$\Rightarrow r=\dfrac{k}{2+\theta }..........\left( 1 \right)$
Let A be the area of the sector, then we get
$\Rightarrow A=\dfrac{1}{2}{{r}^{2}}\theta $
Now put the value of r from equation (1) in the above equation, we get
$\Rightarrow A=\dfrac{1}{2}\cdot \dfrac{{{k}^{2}}}{{{\left( 2+\theta \right)}^{2}}}\cdot \theta $
Now on differentiating on both sides with respect to $\theta $, we get
$\begin{align}
  & \Rightarrow \dfrac{dA}{d\theta }=\dfrac{{{k}^{2}}}{2}\left\{ \dfrac{{{\left( \theta +2 \right)}^{2}}-2\theta \left( \theta +2 \right)}{{{\left( \theta +2 \right)}^{4}}} \right\} \\
 & \Rightarrow \dfrac{dA}{d\theta }=\dfrac{{{k}^{2}}}{2}\dfrac{\left( 2-\theta \right)}{{{\left( \theta +2 \right)}^{3}}} \\
\end{align}$
For maximum area, put $\dfrac{dA}{d\theta }=0$
\[\begin{align}
  & \Rightarrow 0=\dfrac{{{k}^{2}}}{2}\dfrac{\left( 2-\theta \right)}{{{\left( \theta +2 \right)}^{3}}} \\
 & \Rightarrow \theta =2 \\
\end{align}\]
Now again differentiating $\dfrac{dA}{d\theta }=\dfrac{{{k}^{2}}}{2}\dfrac{\left( 2-\theta \right)}{{{\left( \theta +2 \right)}^{3}}}$, we get
$\begin{align}
  & \Rightarrow \dfrac{{{d}^{2}}A}{d{{\theta }^{2}}}=\dfrac{{{k}^{2}}}{2}\left[ \dfrac{2\times \left( -3 \right)}{{{\left( \theta -2 \right)}^{4}}}-\dfrac{{{\left( \theta +2 \right)}^{3}}\times 1-\theta \times 3{{\left( \theta +2 \right)}^{2}}}{{{\left[ {{\left( \theta +2 \right)}^{3}} \right]}^{2}}} \right] \\
 & \Rightarrow \dfrac{{{d}^{2}}A}{d{{\theta }^{2}}}=\dfrac{{{k}^{2}}}{2}\left[ \dfrac{-6}{{{\left( \theta +2 \right)}^{4}}}-\dfrac{\theta +2-3\theta }{{{\left( \theta +2 \right)}^{4}}} \right] \\
 & \Rightarrow \dfrac{{{d}^{2}}A}{d{{\theta }^{2}}}=\dfrac{-{{k}^{2}}}{2}\left[ \dfrac{6}{{{\left( \theta +2 \right)}^{4}}}+\dfrac{2-\theta }{\left| {{\left( \theta +2 \right)}^{4}} \right|} \right] \\
\end{align}$
Now for maximum we already find out the value of $\theta =2$ , now put this value of $\theta $ in the above equation, we get
$\begin{align}
  & \Rightarrow \dfrac{{{d}^{2}}A}{d{{\theta }^{2}}}=\dfrac{-{{k}^{2}}}{2}\left[ \dfrac{6}{{{4}^{4}}}+0 \right] \\
 & \Rightarrow \dfrac{{{d}^{2}}A}{d{{\theta }^{2}}}=\dfrac{-3{{k}^{2}}}{256} \\
\end{align}$
Therefore the above value is greater than zero.
Hence the area is maximum, when $\theta ={{2}^{c}}$.

So, the correct answer is “Option D”.

Note: We can go wrong in the calculation part. Here to differentiate the area we use the quotient rule of differentiation which is as: $\dfrac{d\left( \dfrac{u}{v} \right)}{dx}=\dfrac{u\grave{\ }v-v\grave{\ }u}{{{v}^{2}}}$ on both times . in $\theta ={{2}^{c}}$where c is the constant positive value.