
The perimeter of a right triangle is 23cm. if its hypotenuse is 10cm, find its area.

Answer
567.9k+ views
Hint:
From the question perimeter of the triangle is given that is 24cm from this we can derive relation between a and b then. After that it is well know that ${\left( {hypotenuse} \right)^2} = {\left( {base} \right)^2} + {\left( {perpendicular} \right)^2}$ and then we can find the sides of triangle. Hence, we can calculate the area of the triangle $\dfrac{1}{2} \times altitude \times base$.
Complete step by step solution:
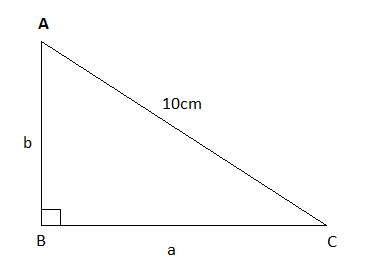
In right $\Delta ABC$ AC=10cm AB=b and BC=a
Perimeter of triangle is 24cm
$ \Rightarrow a + b + 10 = 24$
$ \Rightarrow a + b = 14$
Therefore, $b = 14 - a$
Since it is right angled triangle so
${\left( {hypotenuse} \right)^2} = {\left( {base} \right)^2} + {\left( {perpendicular} \right)^2}$
${\left( {AC} \right)^2} = {\left( {AB} \right)^2} + {\left( {BC} \right)^2}$
$ \Rightarrow {\left( {10} \right)^2} = {\left( b \right)^2} + {\left( a \right)^2}$
Substituting $b = 14 - a$
\[ \Rightarrow 100 = {\left( {14 - a} \right)^2} + {\left( a \right)^2}\]
$ \Rightarrow 2{a^2} - 28a + 96 = 0$
$ \Rightarrow {a^2} - 14a + 48 = 0$
Now, using factorization method
$ \Rightarrow {a^2} - 6a - 8a + 48 = 0$
$ \Rightarrow a\left( {a - 6} \right) - 8\left( {a - 6} \right) = 0$
Taking common $\left( {a - 6} \right)$
$ \Rightarrow \left( {a - 6} \right)\left( {a - 8} \right) = 0$
If $\left( {a - 6} \right) = 0$, then $a = 6cm$
And if $\left( {a - 8} \right) = 0$ then $a = 8cm$
Then value of b= 8cm, 6cm
Now area of $\Delta ABC$ is $\dfrac{1}{2} \times altitude \times base$ where base = 8cm and altitude=6cm
Area =$\dfrac{1}{2} \times 6 \times 8c{m^2}$
Area=$24c{m^2}$
Note:
1) Sum of all the sides is called perimeter.
2) In right-angled triangle ${\left( {hypotenuse} \right)^2} = {\left( {base} \right)^2} + {\left( {perpendicular} \right)^2}$.
3) Area of the triangle is $\dfrac{1}{2} \times altitude \times base$.
4) Never forget to mention units of the quantity.
From the question perimeter of the triangle is given that is 24cm from this we can derive relation between a and b then. After that it is well know that ${\left( {hypotenuse} \right)^2} = {\left( {base} \right)^2} + {\left( {perpendicular} \right)^2}$ and then we can find the sides of triangle. Hence, we can calculate the area of the triangle $\dfrac{1}{2} \times altitude \times base$.
Complete step by step solution:

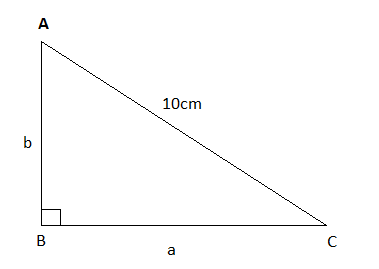
In right $\Delta ABC$ AC=10cm AB=b and BC=a
Perimeter of triangle is 24cm
$ \Rightarrow a + b + 10 = 24$
$ \Rightarrow a + b = 14$
Therefore, $b = 14 - a$
Since it is right angled triangle so
${\left( {hypotenuse} \right)^2} = {\left( {base} \right)^2} + {\left( {perpendicular} \right)^2}$
${\left( {AC} \right)^2} = {\left( {AB} \right)^2} + {\left( {BC} \right)^2}$
$ \Rightarrow {\left( {10} \right)^2} = {\left( b \right)^2} + {\left( a \right)^2}$
Substituting $b = 14 - a$
\[ \Rightarrow 100 = {\left( {14 - a} \right)^2} + {\left( a \right)^2}\]
$ \Rightarrow 2{a^2} - 28a + 96 = 0$
$ \Rightarrow {a^2} - 14a + 48 = 0$
Now, using factorization method
$ \Rightarrow {a^2} - 6a - 8a + 48 = 0$
$ \Rightarrow a\left( {a - 6} \right) - 8\left( {a - 6} \right) = 0$
Taking common $\left( {a - 6} \right)$
$ \Rightarrow \left( {a - 6} \right)\left( {a - 8} \right) = 0$
If $\left( {a - 6} \right) = 0$, then $a = 6cm$
And if $\left( {a - 8} \right) = 0$ then $a = 8cm$
Then value of b= 8cm, 6cm
Now area of $\Delta ABC$ is $\dfrac{1}{2} \times altitude \times base$ where base = 8cm and altitude=6cm
Area =$\dfrac{1}{2} \times 6 \times 8c{m^2}$
Area=$24c{m^2}$
Note:
1) Sum of all the sides is called perimeter.
2) In right-angled triangle ${\left( {hypotenuse} \right)^2} = {\left( {base} \right)^2} + {\left( {perpendicular} \right)^2}$.
3) Area of the triangle is $\dfrac{1}{2} \times altitude \times base$.
4) Never forget to mention units of the quantity.
Recently Updated Pages
Master Class 8 Social Science: Engaging Questions & Answers for Success

Master Class 8 English: Engaging Questions & Answers for Success

Class 8 Question and Answer - Your Ultimate Solutions Guide

Master Class 8 Maths: Engaging Questions & Answers for Success

Master Class 8 Science: Engaging Questions & Answers for Success

Master Class 9 General Knowledge: Engaging Questions & Answers for Success

Trending doubts
What is BLO What is the full form of BLO class 8 social science CBSE

Citizens of India can vote at the age of A 18 years class 8 social science CBSE

Full form of STD, ISD and PCO

Advantages and disadvantages of science

Right to vote is a AFundamental Right BFundamental class 8 social science CBSE

What are the 12 elements of nature class 8 chemistry CBSE




