Question

The perimeter of a rhombus with one diagonal 24 cm long is the same as the perimeter of an equilateral triangle with side 20 cm. Find the length of the other diagonal (in cm).

Answer 1

Hint: First, we will use the perimeter of a rhombus is the same of all sides of the rhombus and then we will use the diagonal bisect each other at 90 degrees to apply the Pythagoras theorem.

Complete step-by-step answer:
We are given that the perimeter of a rhombus with one diagonal 24 cm long is the same as the perimeter of an equilateral triangle with side 20 cm.

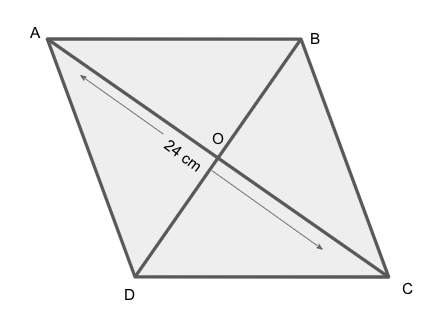
Let us assume that the side of the rhombus is equal to \[l\].
We know that the perimeter of a rhombus is the same of all sides of the rhombus.
Since the sides of a rhombus are equal, so we have
\[
   \Rightarrow l + l + l + l \\
   \Rightarrow 4l \\
 \]
Using the given condition, we will have
\[
   \Rightarrow 3 \times 20 = 4l \\
   \Rightarrow 60 = 4l \\
 \]
Dividing the above equation on both sides by 4, we get
\[
   \Rightarrow \dfrac{{60}}{4} = \dfrac{{4l}}{4} \\
   \Rightarrow 15 = l \\
   \Rightarrow l = 15 \\
   \Rightarrow AB = 15{\text{ cm ......eq.(1)}} \\
 \]
Since we know that the diagonal bisect each other AC is 24, we can get AO dividing it by 2, we get
\[
   \Rightarrow AO = \dfrac{{24}}{2} \\
   \Rightarrow AO = 12{\text{ cm ......eq.(2)}} \\
 \]
Now we will take triangle \[AOB\],
Since we know that the diagonal bisect each other at 90 degrees, we apply the Pythagoras theorem, we get
\[ \Rightarrow A{O^2} + O{B^2} = A{B^2}\]
From equation (1) and equation (2) in the above expression, we get
\[
   \Rightarrow {12^2} + O{B^2} = {15^2} \\
   \Rightarrow 144 + O{B^2} = 225 \\
 \]
Subtracting the above equation by 144 on both sides, we get
\[
   \Rightarrow 144 + O{B^2} - 144 = 225 - 144 \\
   \Rightarrow O{B^2} = 81 \\
 \]
Taking square root both sides in the above equation, we get
\[
   \Rightarrow OB = \pm \sqrt {81} \\
   \Rightarrow OB = \pm 9 \\
 \]
Since the length can never be negative, so the negative value of OB is discarded.
Thus, OB is 9.
Now we know that the diagonal BD is twice the OB, so we have
\[
   \Rightarrow BD = 2\left( 9 \right) \\
   \Rightarrow BD = 18 \\
 \]

Therefore, the length of the diagonal is 18 cm.

Note: Do not forget to write the units with the final answer. In solving these types of questions, formulae should be used to compute the area of a rhombus where sides of the diagonal are given. One mistake that students make is considering the length of diagonals of a rhombus as the same, which is never true. The length of the diagonal of a rhombus is not the same. We know that lengths of the diagonals of squares are equal.