Question

The perimeter of a rectangular table is 28 meters, whereas its area is $ 48{\text{ }}{{\text{m}}^2} $ . What is the length of its diagonal?
A.5 meters
B.10 meters
C.12 meters
D.12.5 meters

Answer 1

Hint: In this question, we need to determine the length of the diagonal of the rectangular table such that the perimeter of a rectangular table is 28 meters, whereas its area is $ 48{\text{ }}{{\text{m}}^2} $ . For this, we will use the formulae for the area and the perimeter of the rectangle along with the properties of the rectangle.

Complete step-by-step answer:
Let the length and the width of the rectangle be denoted as $ l $ and $ b $ respectively.

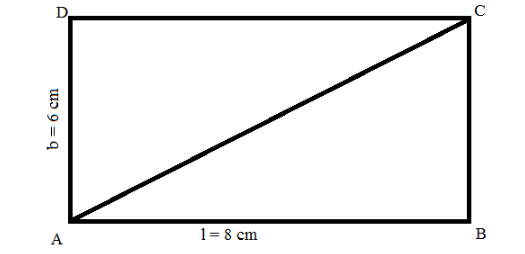
The perimeter of the rectangle is twice the sum of the length and the width of the rectangle. Mathematically, $ P = 2\left( {l + b} \right) $ .
According to the question, the perimeter of the rectangle is 28 meters. So, we can write
 $
  P = 28 \\
   \Rightarrow 2(l + b) = 28 \\
   \Rightarrow l + b = 14 - - - - (i) \;
  $
The area of the rectangle is given as the product of the length and the width. Mathematically, $ A = lb $
Also, it has been given that the area of the rectangle is $ 48{\text{ }}{{\text{m}}^2} $ . So, we can write
 $
  A = 48 \\
  lb = 48 - - - - (ii) \\
  $
From the equation (i), we can write
 $
  l + b = 14 \\
   \Rightarrow l = 14 - b - - - - (iii) \;
  $
Substituting the value from the equation (iii) in the equation (ii), we get
 $
  lb = 48 \\
   \Rightarrow (14 - b)b = 48 \\
   \Rightarrow {b^2} - 14b + 48 = 0 \\
   \Rightarrow {b^2} - 8b - 6b + 48 = 0 \\
   \Rightarrow b(b - 8) - 6(b - 8) = 0 \\
   \Rightarrow (b - 6)(b - 8) = 0 \;
  $
Hence, the length and the width of the rectangular table is 8 cm and 6 cm respectively.
Now, from the above figure, applying Pythagoras theorem in the triangle ABC, we get
 $
  {\left( {AC} \right)^2} = {\left( {AB} \right)^2} + {\left( {BC} \right)^2} \\
   = {\left( 8 \right)^2} + {\left( 6 \right)^2} \\
   = 64 + 36 \\
   = 100 \;
  $
Taking square root to both sides of the above equation, we get
 $
  {\left( {AC} \right)^{\dfrac{1}{2} \times 2}} = \sqrt {100} \\
   = 10 \;
  $
Hence, the length of the diagonal of the rectangular table is 10 cm.
So, the correct answer is “Option B”.

Note: It is worth noting here that the units of the perimeter and the area of the rectangular table are the same and so we have not done any changes. However, if there are different units involved then, we must transform any one unit to another one and carry the calculation. Moreover, we have used the property of the rectangle that the opposite sides are parallel and equal to a rectangle.