Question

The perimeter of a rectangular garden is $368$ feet. If the length of the garden is $97$ feet, what is the width?

Answer 1

Hint: In this question we have to use the formula of perimeter of rectangle i.e. $2\left( {l + b} \right)$ to find the width of a rectangular garden. In the above question, we have given the perimeter and the length of the garden. We have to put these values in the formula and find the answer.

Formula used:
Perimeter of rectangle $ = 2\left( {l + b} \right)$
Where, $l$ is the length of the rectangle and $b$ is the breath of the rectangle.

Complete step by step answer:

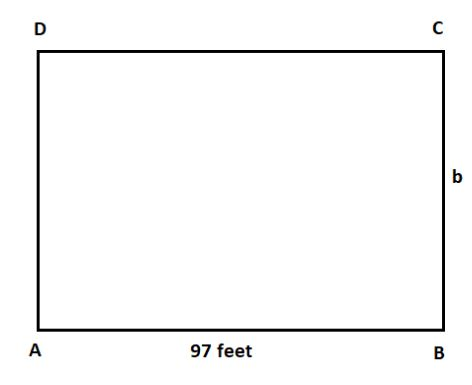
In the above question, we have given the perimeter and the length of the rectangular garden as $368$ feet and $97$ feet respectively and we have to find the width of it. Therefore, we will use the formula of the perimeter of the rectangle to find the width of the rectangular garden.
Perimeter of rectangular garden $ = 2\left( {l + b} \right)$
Now substituting the values of perimeter and length.
$ \Rightarrow 368 = 2\left( {97 + b} \right)$
Now dividing both the equations by $2$.
$ \Rightarrow \dfrac{{368}}{2} = \dfrac{{2\left( {97 + b} \right)}}{2}$
$ \Rightarrow 184 = 97 + b$
$ \Rightarrow b = 184 - 97$
$ \therefore b = 87\,feet$

Therefore, the width of the rectangular garden in $87\,feet$.

Note: We can also do this question without using the formulas. We can do this with the help of properties only. We know that the sum of all sides of any polygon (in this case rectangle) is known as perimeter. We also know that opposite sides of the rectangle are equal. Therefore, we have to add both sides twice to get to the perimeter.