
The perimeter of a rectangle is 13 cm and its width is $2\dfrac{3}{4}{\text{ cm}}$. Find its length.
Answer
606.9k+ views
Hint: In this question the perimeter of the rectangle is given to us and one of the sides is also known. So directly use the basic formula for the perimeter of the rectangle which is $s = 2\left( {l + b} \right)$where s is the perimeter, to obtain the unknown side.
Complete step-by-step answer:
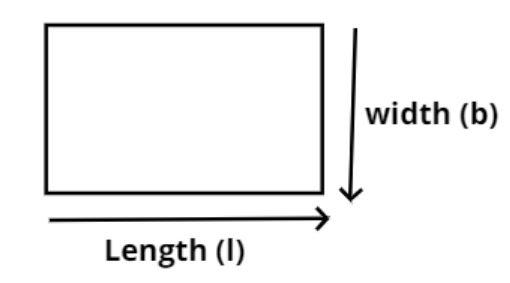
Given data
Perimeter (s) of the rectangle $ = 13{\text{ cm}}$.
Width (b) of the rectangle $2\dfrac{3}{4}{\text{ cm}}$.
Now we have to calculate the length (l) of the rectangle.
So as we know that the perimeter of any shape is the sum of its all sides.
So from figure the perimeter of the rectangle is
$s = 2\left( {l + b} \right)$…………………… (1)
Now covert the width of the rectangle into improper fraction,
$b = 2\dfrac{3}{4} = \dfrac{{\left( {2 \times 4} \right) + 3}}{4} = \dfrac{{11}}{4}{\text{ cm}}$
Now substitute these values in equation (1) we have,
$s = 2\left( {l + b} \right)$
$ \Rightarrow 13 = 2\left( {l + \dfrac{{11}}{4}} \right)$
Divide by 2 in above equation we have,
$ \Rightarrow \dfrac{{13}}{2} = l + \dfrac{{11}}{4}$
Now simplify the above equation we have,
$ \Rightarrow l = \dfrac{{13}}{2} - \dfrac{{11}}{4} = \dfrac{{26}}{4} - \dfrac{{11}}{4} = \dfrac{{15}}{4}{\text{ cm}}$
So, the length of the rectangle is$\dfrac{{15}}{4}{\text{ cm}}$.
So, this is the required answer.
Note: Whenever we face such types of problems the key concept is simply to have the good gist of the basic perimeter formula of rectangle. This understanding of direct formula will help you get on the right track to reach the required entity.
Complete step-by-step answer:

Given data
Perimeter (s) of the rectangle $ = 13{\text{ cm}}$.
Width (b) of the rectangle $2\dfrac{3}{4}{\text{ cm}}$.
Now we have to calculate the length (l) of the rectangle.
So as we know that the perimeter of any shape is the sum of its all sides.
So from figure the perimeter of the rectangle is
$s = 2\left( {l + b} \right)$…………………… (1)
Now covert the width of the rectangle into improper fraction,
$b = 2\dfrac{3}{4} = \dfrac{{\left( {2 \times 4} \right) + 3}}{4} = \dfrac{{11}}{4}{\text{ cm}}$
Now substitute these values in equation (1) we have,
$s = 2\left( {l + b} \right)$
$ \Rightarrow 13 = 2\left( {l + \dfrac{{11}}{4}} \right)$
Divide by 2 in above equation we have,
$ \Rightarrow \dfrac{{13}}{2} = l + \dfrac{{11}}{4}$
Now simplify the above equation we have,
$ \Rightarrow l = \dfrac{{13}}{2} - \dfrac{{11}}{4} = \dfrac{{26}}{4} - \dfrac{{11}}{4} = \dfrac{{15}}{4}{\text{ cm}}$
So, the length of the rectangle is$\dfrac{{15}}{4}{\text{ cm}}$.
So, this is the required answer.
Note: Whenever we face such types of problems the key concept is simply to have the good gist of the basic perimeter formula of rectangle. This understanding of direct formula will help you get on the right track to reach the required entity.
Recently Updated Pages
Master Class 8 Social Science: Engaging Questions & Answers for Success

Master Class 8 Maths: Engaging Questions & Answers for Success

Master Class 8 Science: Engaging Questions & Answers for Success

Class 8 Question and Answer - Your Ultimate Solutions Guide

Master Class 8 English: Engaging Questions & Answers for Success

Master Class 11 Economics: Engaging Questions & Answers for Success

Trending doubts
What is BLO What is the full form of BLO class 8 social science CBSE

Citizens of India can vote at the age of A 18 years class 8 social science CBSE

Full form of STD, ISD and PCO

Right to vote is a AFundamental Right BFundamental class 8 social science CBSE

Summary of the poem Where the Mind is Without Fear class 8 english CBSE

What are gulf countries and why they are called Gulf class 8 social science CBSE




