Question

The percentage of the world population of countries is given in the following table. Find the value of ‘a’. If a pie diagram is to be drawn, what would be the measure of the central angle for the USA?

Country	India	China	Russia	USA	Others	Total
Percentage of population.	15	20	a	a	25	100

Answer 1

Hint: Using the given data we first need to find the value of ‘a’ then we can find the central angle component. Pie chart is a type of graph that displays the data in a circular graph. The entire “pie” represents \[100\% \] of the whole, while the pie “slices” represent a portion of the whole. We know \[{\text{Central angel of component = }}\dfrac{{{\text{Component value}}}}{{{\text{Sum of all components}}}} \times {360^0}\] . Using this we can find the central angle.

Complete step-by-step answer:
Now, we need to find ‘a’.
Sum of percentage of population = 100
That is \[ \Rightarrow 15 + 20 + a + a + 25 = 100\]
 \[ \Rightarrow 60 + 2a = 100\]
 \[ \Rightarrow 2a = 100 - 60\]
 \[ \Rightarrow 2a = 40\]
 \[ \Rightarrow a = \dfrac{{40}}{2}\]
 \[ \Rightarrow a = 20\]
Percentage of population in Russia and the USA is 20.
Now, using \[{\text{Central angel of component = }}\dfrac{{{\text{Component value}}}}{{{\text{Sum of all components}}}} \times {360^0}\] . We get:
 \[ \bullet \] Central angle of India \[ = \dfrac{{15}}{{100}} \times {360^0}\]
 \[ = \dfrac{3}{2} \times 36\]
 \[ = 3 \times 18\]
 \[ = {54^0}\]
 \[ \bullet \] Central angle of China \[ = \dfrac{{20}}{{100}} \times {360^0}\]
 \[ = \dfrac{1}{5} \times 360\]
  \[ = {72^0}\]
  \[ \bullet \] Central angle of USA \[ = \dfrac{{20}}{{100}} \times {360^0}\]
  \[ = \dfrac{1}{5} \times 360\]
  \[ = {72^0}\]
Since we have the same component in Russia I.e., 20.
 \[ \bullet \] Central angel of Russia \[ = {72^0}\]
 \[ \bullet \] Central angel of others \[ = \dfrac{{25}}{{100}} \times {360^0}\]
 \[ = \dfrac{1}{4} \times 360\]
 \[ = 90\]
Drawing a pie chart we get:

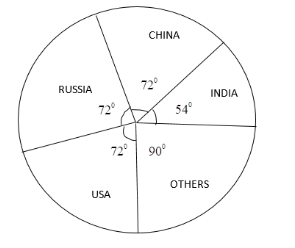
Therefore the Central angle of the USA \[ = {72^0}\] .

Note: Since a pie chart is like a circle, a whole circle contains 360 degrees. You can check if your answer is correct or not. Firstly add all the percentages and substituting the value of ‘a’ you get a total of 100. You can also add all the angels that you have calculated you will obtain 360 degrees. In above we have plotted the pie chart for both percentage and angel.