Question

The particle of a medium vibrates about their mean position whenever a wave travels through that medium. The phase difference between the vibrations of two such particles
A. Varies with time only
B. Varies with the distance separating them only
C. Varies with time as well as distance
D. Is always zero

Answer 1

Hint: The phase difference is the difference in the phase angle of the two waves. The path difference is the difference in the path traversed by the two waves. This problem can directly be solved using the formula that relates the phase difference and the path difference of the wave.
Formula used:
\[\Delta \Phi =\dfrac{2\pi }{\lambda }\Delta x\]

Complete step-by-step solution:
From the given information, we have the data as follows.
The particle of a medium vibrates about its mean position whenever a wave travels through that medium.

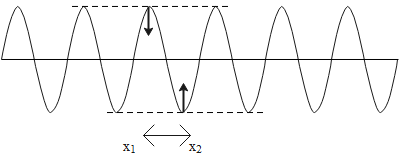
Consider wave travelling through a medium. Let the particle present at the first point (mean position) be such that its velocity is acting in the downward direction as shown in the above figure. Similarly, let the particle present at the second point (mean position) be such that its velocity is acting in the upward direction as shown in the above figure.
Because of the downward and upward-directed velocities, there occurs the path difference between the particles of a wave. And this path difference is given as follows.
\[\Delta x={{x}_{2}}-{{x}_{1}}\]
The formula that represents the phase difference between the vibrations of a wave is given as follows.
\[\Delta \Phi =\dfrac{2\pi }{\lambda }\Delta x\]
Where \[\Delta \Phi \] is the phase difference between the 2 waves, \[\lambda \] is the wavelength and \[\Delta x\] is the path difference between the 2 waves.
Now substitute the expression of the path difference obtained in the above equation.
\[\begin{align}
  & \Delta \Phi =\dfrac{2\pi }{\lambda }({{x}_{2}}-{{x}_{1}}) \\
 & \Rightarrow \Delta \Phi \propto ({{x}_{2}}-{{x}_{1}}) \\
\end{align}\]
Thus, the phase difference between the vibrations of two such particles varies only with the distance separating them.
\[\therefore \] The phase difference between the vibrations of two such particles varies with the distance separating them only, thus, option (B) is correct.

Note: This problem can also be solved using the formula that relates the phase difference with the path difference. The unit of the phase difference is radians and/or can be in degrees. The relation between the phase difference and the path difference holds good only for the 2 waves with the same frequency.