Question

The parallel sides of trapezium are 6cm and 8cm. If the distance between them is 4cm, its area is
A.28 sq.cm
B.24 sq.cm
C.82 sq.cm
D.42 sq.cm

Answer 1

Hint: In this question, we need to evaluate the area of the trapezium such that the parallel sides of trapezium are 6 cm and 8 cm. For this, we will use the relation between area, length of the parallel sides and length between the parallel sides.

Complete step-by-step answer:
Given the length of the parallel sides of trapezium
 \[{L_1} = 6\;cm\] and \[{L_2} = 8\;cm\]
The distance between the parallel sides $D = 4\;cm$
Let us first draw a trapezium from the above given data

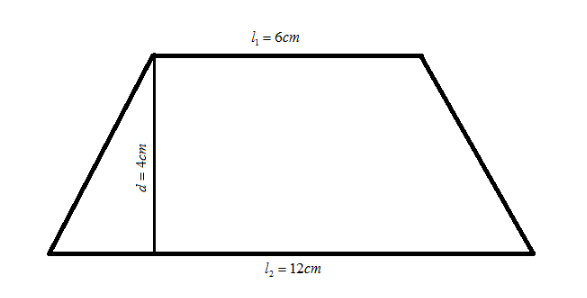
Now we already know the formula for the area of the trapezium which is equal to the product of the sum of parallel sides and distance between them multiplied by half as \[\dfrac{1}{2} \times \left( {{\text{sum of parallel sides}}} \right) \times \left( {{\text{distnace between parallel sides}}} \right)\]
 \[
  Area = \dfrac{1}{2} \times \left( {6 + 8} \right) \times 4 \\
   = \dfrac{1}{2} \times \left( {14} \right) \times 4 \\
   = 7 \times 4 \\
   = 28\;c{m^2} \;
 \]
Hence, the area of trapezoid whose parallel sides are 6cm and 8cm and the distance between them is 4 cm is \[ = 28\;c{m^2}\]
Option A is correct.
So, the correct answer is “Option A”.

Note: When a trapezoid has non parallel sides then the figure is known as irregular trapezoid then to find the area of the trapezoid we divide that geometric figure into a regular triangles or rectangles to find the area of the figure. The area of a trapezium is equal to the product of the sum of the parallel sides and the distance between them multiplied by the half which is given as \[\dfrac{1}{2} \times \left( {{\text{sum of parallel sides}}} \right) \times \left( {{\text{distnace between parallel sides}}} \right)\] .