Question

The paint in a certain container is sufficient to paint an area equal to \[9.375{{m}^{2}}\]. How many bricks of dimensions \[22.5cm\times 10cm\times 7.5cm\] can be painted out of this container?

Answer 1

Hint: We solve this question surface area concept. First we have to find the surface area of the brick. And then we will convert the surface area of the container and surface area of the brick with the same metrics. And then we apply the formula and by simplifying we will find the number of bricks we can paint.

Complete step by step solution:
Let us know about surface area.
Surface area: It is a measure of the total area that the surface of the object occupies. It is always measured in square units. Hence we can also refer to surface area as total surface area TSA.
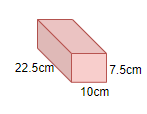
Generally the dimensions are given as \[l\times b\times h\]
Given the dimensions are \[22.5cm\times 10cm\times 7.5cm\]
So the dimensions of brick as
\[l=22.5cm\]
\[b=10cm\]
\[h=7.5cm\]

Now we will calculate the surface area of the brick.
The formula to find the surface area is
\[2\left( lb+bh+lh \right)\]
Now we will substitute values to find the surface area of brick. We will get
\[\Rightarrow 2\left( 22.5\times 10+10\times 7.5+22.5\times 7.5 \right)\]
Now we have to simplify the above expression. We will get
\[\Rightarrow 2\left( 225+75+168.75 \right)\]
After adding we will get
\[\Rightarrow 2\left( 468.75 \right)\]
Now we will remove the parentheses by multiplying with 2.
 \[\Rightarrow 937.5c{{m}^{2}}\]
So the surface area of the brick is \[937.5c{{m}^{2}}\].
Given surface area of container is \[9.375{{m}^{2}}\]
Now we have to convert \[{{m}^{2}}\] into \[c{{m}^{2}}\]. We will get
\[\Rightarrow 9.375\times 100\times 100c{{m}^{2}}\]
By simplifying we get
\[\Rightarrow 937500c{{m}^{2}}\]
Now we have to calculate the number of bricks.
Number of bricks that can be painted = \[\dfrac{\text{surface} \text{ area} \text{ of} \text{ container}}{\text{surface} \text{ area} \text{ of} \text{ brick}}\]
We have
Surface area of container =\[93750c{{m}^{2}}\]
Surface area of brick is = \[937.5c{{m}^{2}}\]
No of bricks painted is = \[\dfrac{93750c{{m}^{2}}}{937.5c{{m}^{2}}}\]
No of bricks painted is = \[\dfrac{937500c{{m}^{2}}}{9375c{{m}^{2}}}\]
Now we have to simplify it we will get
\[=100\]
So the number of bricks that can be painted are \[100\].

Note: We have to be aware of surface area formulas and also the converting techniques. If we don’t convert both into one metric then we will get a different result. Also we have to know the formula for the number of bricks otherwise we cannot solve this question.