
The paint in a certain container is sufficient to paint an area equal to .How many bricks of dimensions \[22.5cm \times 10cm \times 7.5cm\] can be painted out of this container?
Answer
582k+ views
Hint: Total surface area:Total surface area refers to the area including the base(s) and the curved part. It is the total area covered by the surface of the object. If the shape has a curved surface and base, then the total area will be the sum of the two areas.
The total surface area (TSA) of a cuboid is the sum of the areas of its 6 faces, which is given by:
Formula used:Total Surface Area (TSA) = \[2(lw + wh + hl)\]
Complete step by step answer:
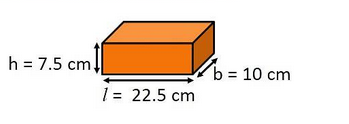
Dimension of brick are: \[l = 22.5cm,b = 10cm,c = 7.5cm\]
Total surface area of a container= \[9.375{m^2} = 9.375 \times {({10^2})^2}c{m^2} = 93750c{m^2}\]
Total surface area of a brick =\[2(lb + bh + hl)\]
= \[2\left( {22.5 \times 10 + 10 \times 7.5 + 7.5 \times 22.5} \right)\]
= \[2 \times 468.75c{m^2}\]
\[ = 937.5c{m^{^2}}\]
Number of bricks that painted out of this container=\[\dfrac{{{\text{total area painted by containers paint}}}}{{{\text{total surface area of a brick}}}}\]
=\[\dfrac{{93750}}{{937.5}} = 100\]
100 bricks can be painted out by the paint of the container.
Note:
To find no. of bricks Units should be the same. In above question dimensions of brick are in whereas dimensions of containers are in $m$. To solve questions we should convert to or to. Students make mistakes in the unit. If units are not the same, the answer will be incorrect.
Another confusion topic is about surface area and total surface area. In the above question, we use the formula of total surface area instead of surface area because all 6 faces of brick will paint.
Surface area relates to 2-dimensional shapes like rectangles, triangles, circles which are regular shapes. Total surface area relates to 3-dimensional objects - cuboids, pyramids, prisms, spheres etc.
Curved surface area/Lateral surface area:Curved surface area refers to the area of only the curved part of the shape excluding its base(s). It is also referred to as lateral surface area for shapes such as a cylinder.
Following table indicates the difference between surface area and total surface area.
The total surface area (TSA) of a cuboid is the sum of the areas of its 6 faces, which is given by:
Formula used:Total Surface Area (TSA) = \[2(lw + wh + hl)\]
Complete step by step answer:

Dimension of brick are: \[l = 22.5cm,b = 10cm,c = 7.5cm\]
Total surface area of a container= \[9.375{m^2} = 9.375 \times {({10^2})^2}c{m^2} = 93750c{m^2}\]
Total surface area of a brick =\[2(lb + bh + hl)\]
= \[2\left( {22.5 \times 10 + 10 \times 7.5 + 7.5 \times 22.5} \right)\]
= \[2 \times 468.75c{m^2}\]
\[ = 937.5c{m^{^2}}\]
Number of bricks that painted out of this container=\[\dfrac{{{\text{total area painted by containers paint}}}}{{{\text{total surface area of a brick}}}}\]
=\[\dfrac{{93750}}{{937.5}} = 100\]
100 bricks can be painted out by the paint of the container.
Note:
To find no. of bricks Units should be the same. In above question dimensions of brick are in whereas dimensions of containers are in $m$. To solve questions we should convert to or to. Students make mistakes in the unit. If units are not the same, the answer will be incorrect.
Another confusion topic is about surface area and total surface area. In the above question, we use the formula of total surface area instead of surface area because all 6 faces of brick will paint.
Surface area relates to 2-dimensional shapes like rectangles, triangles, circles which are regular shapes. Total surface area relates to 3-dimensional objects - cuboids, pyramids, prisms, spheres etc.
Curved surface area/Lateral surface area:Curved surface area refers to the area of only the curved part of the shape excluding its base(s). It is also referred to as lateral surface area for shapes such as a cylinder.
Following table indicates the difference between surface area and total surface area.
| Geometrical figure | Perimeter | Total surface area | Curved surface area/ lateral surface area | Figure |
| Cuboid | \[4\left( {l + b + h} \right)\] | \[2\left( {lb + bh + hl} \right)\] | \[2h\left( {l + b} \right)\] | 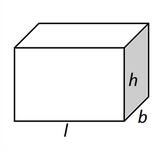
|
| Cube | \[6a\] | \[6{a^2}\] | \[4{a^2}\] | 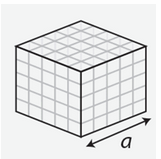
|
| Cylinder | - | \[2\pi r\left( {r + h} \right)\] | \[2\pi rh\] | 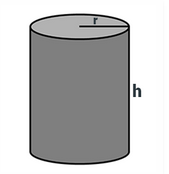
|
Recently Updated Pages
Master Class 11 Computer Science: Engaging Questions & Answers for Success

Master Class 11 Business Studies: Engaging Questions & Answers for Success

Master Class 11 Economics: Engaging Questions & Answers for Success

Master Class 11 English: Engaging Questions & Answers for Success

Master Class 11 Maths: Engaging Questions & Answers for Success

Master Class 11 Biology: Engaging Questions & Answers for Success

Trending doubts
One Metric ton is equal to kg A 10000 B 1000 C 100 class 11 physics CBSE

There are 720 permutations of the digits 1 2 3 4 5 class 11 maths CBSE

Discuss the various forms of bacteria class 11 biology CBSE

Draw a diagram of a plant cell and label at least eight class 11 biology CBSE

State the laws of reflection of light

Explain zero factorial class 11 maths CBSE




