Question

The packing efficiency of the face centred cubic (fcc), body-centred cubic (bcc) and simple primitive cubic (pc) lattices follows the order:
A. fcc > bcc > pc
B. bcc > fcc > pc
C. pc > bcc > fcc
D. bcc > pc > fcc

Answer 1

Hint: We know that each cube has 8 corners, 12 edges, 6 faces, 12 face diagonals and 8 body diagonals. Keeping this information in mind we need to proceed for the comparison.

Step by step answer:
The percentage efficiency of a simple cubic unit cell is:
Suppose,
Length of the unit cell \[\text{= a}\]
Radius of the sphere (atom) \[\text{= r}\]
Total volume of the unit cell \[\text{= }{{\text{a}}^{\text{3}}}\text{= }{{\left( \text{2r} \right)}^{\text{3}}}\text{= 8}{{\text{r}}^{\text{3}}}\]
Number of atoms per unit cell \[\text{= 8 }\!\!\times\!\!\text{ }\dfrac{\text{1}}{\text{8}}\text{ = 1}\]
Volume of the atom \[\text{r = }\dfrac{\text{1}}{\text{2}\sqrt{\text{2}}\text{a}}\]\[\text{= }\dfrac{\text{4}}{\text{3}}\text{ }\!\!\pi\!\!\text{ }{{\text{r}}^{\text{3}}}\]
\[\therefore \]packing fraction \[\text{= }\dfrac{\text{Occupied volume }}{\text{Total volume}}\text{ }\]
\[\text{= }\dfrac{\left( \text{4/3} \right)\text{ }\!\!\pi\!\!\text{ }{{\text{r}}^{\text{3}}}}{\text{8}{{\text{r}}^{\text{3}}}}\text{= 0}\text{.5233}\]
Thus, the percentage of occupied volume or packing efficiency \[\text{= 0}\text{.5233 }\!\!\times\!\!\text{ 100 = 52}\text{.33 }\!\!%\!\!\text{ }\]
The percentage efficiency of a body-centred unit cell is:
Suppose,
Length of the unit cell \[\text{= a}\]
Radius of the sphere (atom) \[\text{= r}\]
In this unit cell,
\[\text{a = }\dfrac{\text{4}}{\sqrt{\text{3}}}\text{ }\!\!\times\!\!\text{ r}\]
Total volume of the unit cell \[\text{= }{{\text{a}}^{\text{3}}}\text{= }{{\left( \dfrac{\text{4}}{\sqrt{\text{3}}} \right)}^{\text{3}}}{{\text{r}}^{\text{3}}}\text{= }\dfrac{\text{64}}{\text{3}\sqrt{\text{3}}}\text{ }{{\text{r}}^{\text{3}}}\]
Number of atoms per unit cell \[\text{= 2}\]
Volume of two atoms \[\text{= 2 }\!\!\times\!\!\text{ }\dfrac{\text{4}}{\text{3}}\text{ }\!\!\pi\!\!\text{ }{{\text{r}}^{\text{3}}}\]
Therefore, packing fraction (3D) \[\text{= }\dfrac{\text{Occupied volume }}{\text{Total volume}}\text{ }\]
\[\text{=}\dfrac{\text{2 }\!\!\times\!\!\text{ }\dfrac{\text{4}}{\text{3}}\text{ }\!\!\pi\!\!\text{ }{{\text{r}}^{\text{3}}}}{\dfrac{\text{64}}{\text{3}\sqrt{\text{3}}}{{\text{r}}^{\text{3}}}}\text{=0}\text{.68}\]

Thus, the percentage of occupied volume or packing efficiency \[\text{= 68 }\!\!%\!\!\text{ }\]
The percentage efficiency of a face-centred cubic unit cell:
Suppose,
Length of the unit cell \[\text{= a}\]
Radius of the sphere (atom) \[\text{= r}\]
In this unit cell,
\[\text{a=2}\sqrt{\text{2}}\times \text{r}\]
Total volume of the unit cell \[\text{=}{{\text{a}}^{\text{3}}}\text{=(2}\sqrt{\text{2}}{{\text{)}}^{\text{3}}}{{\text{r}}^{\text{3}}}\text{=16}\sqrt{\text{2}}{{\text{r}}^{\text{3}}}\]
Number of atoms per unit cell \[\text{= 4}\]
Volume of four atoms \[\text{= 4 }\!\!\times\!\!\text{ }\dfrac{\text{4}}{\text{3}}\text{ }\!\!\pi\!\!\text{ }{{\text{r}}^{\text{3}}}\]
                (This is the occupied volume)
Therefore, packing fraction (3D) \[\text{=}\dfrac{\text{Occupied volume }}{\text{ Total volume}}\]
\[\text{=}\dfrac{\text{4 }\!\!\times\!\!\text{ }\dfrac{\text{4}}{\text{3}}\text{ }\!\!\pi\!\!\text{ }{{\text{r}}^{\text{3}}}}{\text{16}\sqrt{\text{2}}{{\text{r}}^{\text{3}}}}\text{=0}\text{.7401}\]
Thus, the percentage of occupied volume or packing efficiency \[\text{= 74}\text{.01 }\!\!%\!\!\text{ }\]
Hence we can see that the packing efficiency goes in to order:
fcc > bcc > pc
So Option A is the correct answer.

Note:

Atomic radius of simple cubic unit cell is: \[\text{r = }\dfrac{\text{a}}{\text{2}}\]

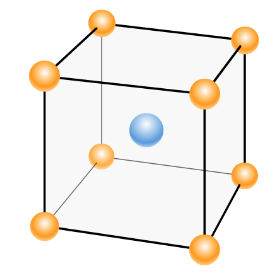
Atomic radius of body-centred unit cell is: \[\text{r = }\dfrac{\sqrt{\text{3}}}{\text{4 a}}\]

Atomic radius of face-centred unit cell is: \[\text{r = }\dfrac{\text{1}}{\text{2}\sqrt{\text{2}}\text{a}}\]