Question

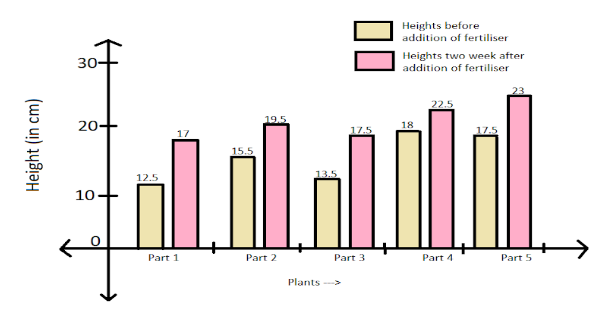
The owner of a plant nursery wanted to test the effectiveness of a new type of fertilizer. He measured the heights of five plants, and then gave each an equal amount of fertilizer. Two weeks later, he measured the heights of the plants again. The graph shows the height of the plants before and after the addition of fertilizer. What was the mean growth of the new plants?

A) $4.5cm$
B) $5cm$
C) $5.5cm$
D) $6cm$

Answer 1

Hint: In this question, we are given a graph in which height of five plants before and after adding the fertilizer has been given. We have been asked the mean growth of the new plants. First, find the growth in plants by subtracting the old height from the new height. Then, put them in the formula of mean. Add all the growth and divide it by 5 as there are 5 plants. You will have your answer.

Complete step-by-step solution:
We are given a graph in which height of five plants before and after adding the fertilizer has been given. It is also shown in the graph that beige color shows the height before fertilizer has been added and pink shows the height after the fertilizer has been added. We have been asked the mean growth of new plants.
We will start by finding the growth of each plant.
Growth in Plant 1 = $17 - 12.5 = 4.5cm$
Growth in Plant 2 = $19.5 - 15.5 = 4cm$
Growth in Plant 3 = $17.5 - 13.5 = 4cm$
Growth in Plant 4 = $22.5 - 18 = 4.5cm$
Growth in Plant 5 = $23 - 17.5 = 5.5cm$
Now, we have the growth of each plant after the fertilizer has been added.
Now, we will find the mean growth.
$ \Rightarrow $ Mean =$\dfrac{{{\text{Sum of observations}}}}{{{\text{No}}{\text{. of observations}}}}$
Putting all the values,
$ \Rightarrow $ Mean =$\dfrac{{4.5 + 4 + 4 + 4.5 + 5.5}}{5}$
Adding the terms we get,
$ \Rightarrow $ Mean =$\dfrac{{22.5}}{5}$
Hence,
$ \Rightarrow $ Mean =$4.5cm$

$\therefore $ The mean growth of the new plants is option A) $4.5cm$.

Note: We have to remember that, a mean is the simple mathematical average of a set of two or more numbers. The mean for a given set of numbers can be computed in more than one way, including the arithmetic mean method, which uses the sum of the numbers in the series, and the geometric mean method, which is the average of a set of products. However, all of the primary methods of computing a simple average produce the same approximate result most of the time.
Many students put the new heights in the formula. You have been asked to mean ‘growth’. So, you have to find the growth first and then put it in the formula. Do not put the new heights directly as it will give the wrong answer.