Question

The opposite angular point of a square is (3, 4) and (1, -1). Find the coordinate of the other two vertices.

Answer 1

Hint: Now we know two opposite vertices of a square. Let us assume the third vertex is (x, y). Now we know that the side of the square is always equal. Hence we will have the distance between (x, y) and (3, 4) is equal to the distance between (1, -1) and (x, y). Now we also know that each angle of the square is 90 degrees. Hence the three points will satisfy the Pythagoras theorem. Hence we will have two equations and two variables. We can solve them simultaneously to find (x, y).

Complete step by step answer:
Now consider a square with its opposite angular points as (3, 4) and (1, -1).
Let these points be A and C respectively. Hence A = (3, 4) and B = (1, -1).
Now let us say the third vertex of the square is C and let C = (x, y).

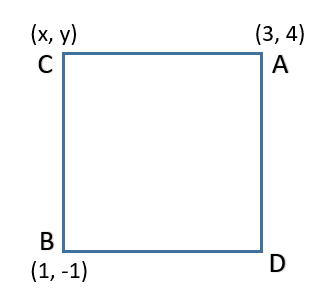
Now we have A = (3, 4), B = (1, -1) and C = (x, y).
Now we know that the sides of squares are equal.
Hence we get AC = BC.
Hence $A{{C}^{2}}=B{{C}^{2}}$
Now we know that distance between points $\left( {{x}_{1}},{{x}_{2}} \right)$ and $\left( {{y}_{1}},{{y}_{2}} \right)$ is given by $\sqrt{{{\left( {{x}_{2}}-{{x}_{1}} \right)}^{2}}+{{\left( {{y}_{2}}-{{y}_{1}} \right)}^{2}}}$
Hence we get
$\begin{align}
  & {{\left( \sqrt{{{\left( x-3 \right)}^{2}}+{{\left( y-4 \right)}^{2}}} \right)}^{2}}={{\left( \sqrt{{{\left( x-1 \right)}^{2}}+{{\left( y-(-1) \right)}^{2}}} \right)}^{2}} \\
 & \Rightarrow {{\left( x-3 \right)}^{2}}+{{\left( y-4 \right)}^{2}}={{\left( x-1 \right)}^{2}}+{{\left( y+1 \right)}^{2}} \\
 & \\
\end{align}$
Now we have ${{\left( a\pm b \right)}^{2}}={{a}^{2}}\pm 2ab+{{b}^{2}}$ using this we get
$\begin{align}
  & {{x}^{2}}+9-6x+{{y}^{2}}+16-8y={{x}^{2}}+1-2x+{{y}^{2}}+1+2y \\
 & \Rightarrow 9-6x+16-8y=1-2x+1+2y \\
 & \Rightarrow 2x-6x-2y-8y+16+9-1-1=0 \\
 & \Rightarrow -4x+10y+23=0 \\
 & \Rightarrow 4x-10y=23 \\
 & \therefore x=\dfrac{23-10y}{4}..............................\left( 1 \right) \\
\end{align}$
Now ABC also form a right angle triangle, such that angle C is 90 degrees
Hence we get
$A{{C}^{2}}+B{{C}^{2}}=A{{B}^{2}}$
Now again we have A = (3, 4), B = (1, -1) and C = (x, y) hence using distance formula we get
$\begin{align}
  & {{\left( \sqrt{{{\left( x-3 \right)}^{2}}+{{\left( y-4 \right)}^{2}}} \right)}^{2}}+{{\left( \sqrt{{{\left( x-1 \right)}^{2}}+{{\left( y-(-1) \right)}^{2}}} \right)}^{2}}=\left( \sqrt{{{(3-1)}^{2}}+{{\left( 4-\left( -1 \right) \right)}^{2}}} \right) \\
 & \Rightarrow {{\left( x-3 \right)}^{2}}+{{\left( y-4 \right)}^{2}}+{{\left( x-1 \right)}^{2}}+{{\left( y+1 \right)}^{2}}={{\left( 2 \right)}^{2}}+{{\left( 5 \right)}^{2}} \\
\end{align}$
Now we know, ${{\left( a\pm b \right)}^{2}}={{a}^{2}}\pm 2ab+{{b}^{2}}$ using this we get
\[\begin{align}
  & {{x}^{2}}+9-6x+{{y}^{2}}+16-8y+{{x}^{2}}+1-2x+{{y}^{2}}+1+2y=25+4=29 \\
 & \Rightarrow 2{{x}^{2}}+2{{y}^{2}}-8x-6y+27=29 \\
 & \Rightarrow 2{{x}^{2}}+2{{y}^{2}}-8x-6y=29-27 \\
 & \Rightarrow 2{{x}^{2}}+2{{y}^{2}}-8x-6y=2 \\
\end{align}\]
Dividing the whole equation by 2 we get.
${{x}^{2}}+{{y}^{2}}-4x-3y=1$
Now substituting the value of x from equation (1) we get.
${{\left( \dfrac{23-10y}{4} \right)}^{2}}+{{y}^{2}}-4\left( \dfrac{23-10y}{4} \right)-3y=1$
$\Rightarrow \dfrac{{{\left( 23-10y \right)}^{2}}}{16}+{{y}^{2}}-23+10y-3y=1$
Now multiplying the whole equation by 16 and using ${{\left( a\pm b \right)}^{2}}={{a}^{2}}\pm 2ab+{{b}^{2}}$ we get
$\begin{align}
  & 529+100{{y}^{2}}-460y+16{{y}^{2}}-368+160y-48y=16 \\
 & \Rightarrow 116{{y}^{2}}-348y-145=0 \\
\end{align}$
Dividing the whole equation by 29 we get
$\begin{align}
  & 4{{y}^{2}}-12y-5=0 \\
 & \Rightarrow 4{{y}^{2}}-2y-10y-5=0 \\
 & \Rightarrow 2y\left( 2y-1 \right)-5\left( 2y-1 \right)=0 \\
 & \Rightarrow \left( 2y-5 \right)\left( 2y-1 \right)=0 \\
\end{align}$
Hence we have $y=\dfrac{5}{2}$ or $y=\dfrac{1}{2}$ .
Now for $y=\dfrac{1}{2}$ we have $x=\dfrac{23-10y}{4}=\dfrac{23-5}{4}=\dfrac{18}{4}=\dfrac{9}{2}$
And if $y=\dfrac{5}{2}$ we have $x=\dfrac{23-10y}{4}=\dfrac{23-25}{4}=\dfrac{-2}{4}=-\dfrac{1}{2}$
Now for $y=\dfrac{1}{2}$ we have $x=\dfrac{9}{2}$ and for $y=\dfrac{5}{2}$ we have $x=-\dfrac{1}{2}$
Hence the other two vertex of square are $\left( -\dfrac{1}{2},\dfrac{5}{2} \right),\left( \dfrac{9}{2},\dfrac{1}{2} \right)$

Note:
Now note that we have just considered one vertex while solving but we got both the vertex. The properties that we used for solving will be satisfied by both the vertex. Hence we get both points. Now we know that diagonals of the square make an angle of 45 degrees with each side. Hence we can also use trigonometric ratios to find the length of a side and then by distance formula find the coordinates.