Question

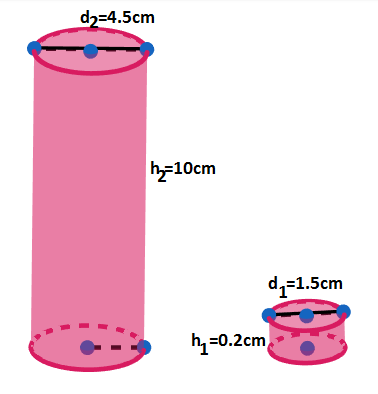
The numbers of coins of 1.5 cm in diameter and 0.2 cm thick, to be melted to form a right circular cylinder of height 10 cm and diameter 4.5 cm is \[\]
A.150\[\]
B.250\[\]
C.450\[\]
D.500\[\]

Answer 1

Hint: We find the volume of a single coin ${{V}_{1}}=\pi {{r}_{1}}^{2}{{h}_{1}}$ where ${{r}_{1}}$ is the radius of the circular face of the coin and ${{h}_{1}}$ is the thickness of the coin. We find the volume of the right circular cylinder ${{V}_{1}}=\pi {{r}_{1}}^{2}{{h}_{1}}$ where ${{r}_{1}}$ is the radius of and ${{h}_{1}}$ is height of right circular cylinder. We assume an $x$ number of coins needed to be melted to make the cylinder. We solve $x{{V}_{1}}={{V}_{2}}$ to get $x$.\[\]

Complete step by step answer:

We know that a cylinder is a solid three dimensional object with one curved surface and two circular plane surfaces called bases. The distance from one base to another is called height of the cylinder and is denoted as $h$ and the radius at the base is denoted as $r$ .
The volume of the cylinder is the amount of space enclosed by cylinder is given by the formula
\[V=\pi {{r}^{2}}h\]
We also know that the radius of circle $r$ is half of diameter $d$ which means.
\[d=\dfrac{r}{2}\]
We are given in the question that the diameter of the cylinder is 1.5 cm in diameter and thickness is 0.2cm. We know that coins are made in cylindrical shape and thickness is measured as the distance between the two circular faces which act as bases for the cylinder. So the thickness is height here. Let us denote the diameter, radius, height and volume of cylindrical coin as ${{d}_{1}},{{r}_{1}},{{h}_{1}},{{V}_{1}}$. So we have ${{d}_{1}}=1.5\text{cm},{{h}_{1}}=0.2\text{cm}$and from the formula of volume of cylinder we have
\[\begin{align}
  & {{V}_{1}}=\pi {{r}_{1}}^{2}{{h}_{1}} \\
 & \Rightarrow {{V}_{1}}=\pi {{\left( \dfrac{{{d}_{1}}}{2} \right)}^{2}}{{h}_{1}} \\
 & \Rightarrow {{V}_{1}}=\pi {{\left( \dfrac{1.5}{2} \right)}^{2}}\times 0.2 \\
\end{align}\]
We are further given the question that to be melted to form a right circular cylinder of height 10 cm and diameter 4.5 cm. Let us denote the diameter, radius, height and volume of circular cylinder as ${{d}_{2}},{{r}_{2}},{{h}_{2}},{{V}_{2}}$. So we have ${{d}_{1}}=4.5\text{cm},{{h}_{1}}=10\text{cm}$ and from the formula of volume of cylinder we have
\[\begin{align}
  & {{V}_{2}}=\pi {{r}_{2}}^{2}{{h}_{2}} \\
 & \Rightarrow {{V}_{2}}=\pi {{\left( \dfrac{{{d}_{2}}}{2} \right)}^{2}}{{h}_{1}} \\
 & \Rightarrow {{V}_{2}}=\pi {{\left( \dfrac{4.5}{2} \right)}^{2}}\times 10 \\
\end{align}\]
 

When we melt the coins its volume will be liquefied and then solidified to make the circular cylinder. So the sum of the volumes of coins is the volume of the cylinder. Let us assume that we need $x$ coins to make the cylinder. So the sum of volumes of $x$ coins is $x$ times the volume of single coin that is $X{{V}_{1}}$ which will be equal to volume of cylinder ${{V}_{2}}$. So we have,
\[\begin{align}
  & x{{V}_{1}}={{V}_{2}} \\
 & \Rightarrow x=\dfrac{{{V}_{2}}}{{{V}_{1}}} \\
\end{align}\]
We put the values obtained for ${{V}_{1}},{{V}_{2}}$ and have,
\[\begin{align}
  & \Rightarrow x=\dfrac{\pi {{\left( \dfrac{4.5}{2} \right)}^{2}}\times 10}{\pi {{\left( \dfrac{1.5}{2} \right)}^{2}}\times 0.2} \\
 & \Rightarrow x=\dfrac{\dfrac{45}{20}\times \dfrac{45}{20}}{\dfrac{15}{20}\times \dfrac{15}{20}\times \dfrac{2}{10}}\times 10=\dfrac{3\times 3\times 10}{2}\times 10=450 \\
\end{align}\]

So, the correct answer is “Option C”.

Note: We note that the question assumes that there is no wastage of volume. The cylinder whose base is a circle is called a circular cylinder. If the height of the circle is perpendicular to base we call the cylinder right cylinder otherwise oblique cylinder. The volume of hollow cylinder with inner radius ${{r}_{1}}$ and outer radius ${{r}_{2}}$ is given by $\pi \left( {{r}_{1}}^{2}-{{r}_{2}}^{2} \right)h$.