Question

The number of votes received in the election of class monitor are
Mona − \[6\] votes,
Payal − \[10\] votes,
Prashant − \[2\] votes,
Sona − \[20\] votes,
Rajen − \[15\] votes,
Meera − \[4\] votes,
Subhash − \[3\] votes
In a circle graph the central angle corresponding to the votes of Sona, Mona, Meera and Subhash are
A. \[{120^ \circ },{36^ \circ },{24^ \circ },{18^ \circ }\]
B. \[{38^ \circ },{115^ \circ },{25^ \circ },{20^ \circ }\]
C. \[{50^ \circ },{30^ \circ },{130^ \circ },{30^ \circ }\]
D. \[{72^ \circ },{36^ \circ },{48^ \circ },{150^ \circ }\]

Answer 1

Hint: n order to draw a circle graph the central angle corresponding to the number of votes received in the election of class monitor. We give a graph representation for the votes of the persons Mona, Payal, Prashant, Sona, Rajen, Meera, Subhash. The graph is given below.

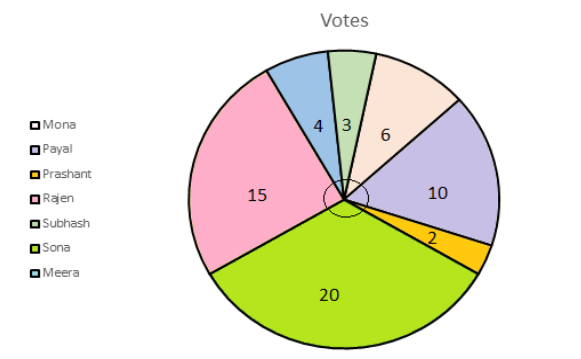
We have to find the central angle corresponding to the various votes can be calculated by \[Angle = \dfrac{{Number{\text{ }}of{\text{ }}votes \times {{360}^ \circ }}}{{Total{\text{ }}number{\text{ }}number{\text{ }}of{\text{ }}votes}}\] .

Complete step by step solution:
In this problem,
The number of votes received in the election of class monitor are
Mona − \[6\] votes,
Payal − \[10\] votes,
Prashant − \[2\] votes,
Sona − \[20\] votes,
Rajen − \[15\] votes,
Meera − \[4\] votes,
Subhash − \[3\] votes
We need to find the central angles corresponding to the various votes, we get
The formula is given as follows, \[Angle = \dfrac{{Number{\text{ }}of{\text{ }}votes \times {{360}^ \circ }}}{{Total{\text{ }}number{\text{ }}number{\text{ }}of{\text{ }}votes}}\]
The total number of votes \[ = 6 + 10 + 2 + 20 + 15 + 4 + 3 = 60\] Votes
Now, we have to find central angles for every person can be calculated by the formula, we can get
Mona \[ = \dfrac{{6 \times {{360}^ \circ }}}{{60}} = 6 \times {6^ \circ } = {36^ \circ }\]
Payal \[ = \dfrac{{10 \times {{360}^ \circ }}}{{60}} = 10 \times {6^ \circ } = {60^ \circ }\]
Prashant \[ = \dfrac{{2 \times {{360}^ \circ }}}{{60}} = 2 \times {6^ \circ } = {12^ \circ }\]
Sona \[ = \dfrac{{20 \times {{360}^ \circ }}}{{60}} = 20 \times {6^ \circ } = {120^ \circ }\]
Rajen \[ = \dfrac{{15 \times {{360}^ \circ }}}{{60}} = 15 \times {6^ \circ } = {90^ \circ }\]
Meera \[ = \dfrac{{4 \times {{360}^ \circ }}}{{60}} = 4 \times {6^ \circ } = {24^ \circ }\]
Subhash \[ = \dfrac{{3 \times {{360}^ \circ }}}{{60}} = 3 \times {6^ \circ } = {18^ \circ }\]
We need the central angle corresponding to the votes of Sona, Mona, Meera and Subhash are \[{120^ \circ },{36^ \circ },{24^ \circ },{18^ \circ }\] .
Therefore, the option (A) is the correct one.
So, the correct answer is “Option A”.

Note: We note that the problem can be calculate the sum of total votes for finding the central angle corresponding to the various votes and we plot a graph for the number of votes having the persons then finding the central angle by the formula we have to remind to solve this kind of problems. The central angle is calculated to find the angle at the centre of a circle whose radii extend towards an arc along the circumference.