Question

The number of students in a hostel, speaking Hindi is 40, Bengali is 25 and English is 35. If it is represented in a pie chart, the central angle corresponding to Hindi is _____
\[\left( a \right){{152}^{\circ }}\]
\[\left( b \right){{72}^{\circ }}\]
\[\left( c \right){{40}^{\circ }}\]
\[\left( d \right){{144}^{\circ }}\]

Answer 1

Hint: To solve this question, we will calculate the total number of students studying any language which is given by 40, 25 and 35 and then by using the formula given as the central angle of any language as \[\dfrac{\text{number of students of that language}}{100}\times {{360}^{\circ }},\] that will give our result.

Complete step by step answer:
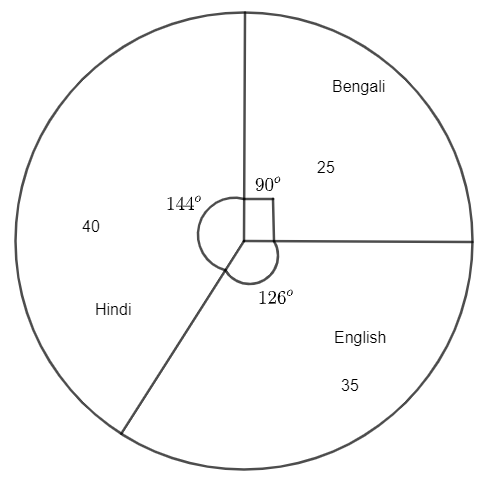
We are given that the number of students in the hostel speaking Hindi is 40. The students speaking Bengali is 25 and the students speaking English is 35. Let us calculate the pie chart central angle corresponding to Hindi by drawing the exact area of them separately.
The total number in the circle will be obtained by adding 40, 25 and 35.
\[\text{Total number in the circle}=40+25+35=100\]
Then the area of Hindi can be obtained by dividing 40 by 100.
\[\Rightarrow \text{Area of Hindi}=\dfrac{40}{100}\]
And the corresponding angle in the degree of the area of Hindi can be calculated by multiplying \[\dfrac{40}{100}\] with \[{{360}^{\circ }}.\]
The central angle of Hindi is given by \[\dfrac{40}{100}\times {{360}^{\circ }}={{144}^{\circ }}.\]
Hence, if the given theory is represented in the pie chart, the central angle corresponding to Hindi is \[{{144}^{\circ }},\]

So, the correct answer is “Option D”.

Note: We can also calculate the central angle in the degree of all other subjects as well. We can also multiply \[\dfrac{25}{100}\] by \[{{360}^{\circ }}\] to get the central angle of Bengali.
\[\Rightarrow \text{Central angle in degree of Bengali}=\dfrac{25}{100}\times {{360}^{\circ }}\]
\[\Rightarrow \text{Central angle in degree of Bengali}=\dfrac{1}{4}\times {{360}^{\circ }}\]
\[\Rightarrow \text{Central angle in degree of Bengali}={{90}^{\circ }}\]
Again, similarly, the central angle in the degree of English is
\[\Rightarrow \dfrac{35}{100}\times {{360}^{\circ }}\]
\[\Rightarrow {{126}^{\circ }}\]