Question

The number of solutions of $\left| {\left[ x \right] - 2x} \right| = 4$ , where [x] is the greatest integer less than or equal to x
A.2
B.4
C.1
D.infinite

Answer 1

Hint: To solve this question we’ll approach the answer by taking two cases. The first case will be when the x is an integer and the second when x is a non integer.
From both cases, we’ll have the different equations and by solving them we’ll have some values, then by counting the number of the solutions of the equation we’ll get the answer.

Complete step-by-step answer:
Given data: $\left| {\left[ x \right] - 2x} \right| = 4$, [x] is the greatest integer function
Case 1: let x be an integer
Therefore we can say that $\left[ x \right] = x$
Substituting the value of $\left[ x \right]$in the given equation
i.e. $\left| {x - 2x} \right| = 4$
On solving the terms of modulus function, we get,
$ \Rightarrow \left| { - x} \right| = 4$
Using $\left| { - z} \right| = \left| z \right|$, we get,
$ \Rightarrow \left| x \right| = 4$
Now, we know that $\left| z \right| = a$, then $z = \pm a$
$\therefore x = \pm 4$
Case II: when x is any positive real number other than integers
lets $x = i + t$, where \[0 < t < 1\] and i is an integer
therefore we can say that, $\left[ x \right] = i$
Now, substituting the value of $\left[ x \right] = i$and $x = i + t$ in the given equation
i.e. $\left| {i - 2\left( {i + t} \right)} \right| = 4$
On simplifying the brackets, we get,
$ \Rightarrow \left| {i - 2i - 2t} \right| = 4$
On Solving for the like terms, we get,
$ \Rightarrow \left| { - i - 2t} \right| = 4$
Taking (-1) common in the modulus function, we get,
$ \Rightarrow \left| { - \left( {i + 2t} \right)} \right| = 4$
Using $\left| { - z} \right| = \left| z \right|$
$ \Rightarrow \left| {i + 2t} \right| = 4$
Now, we know that $\left| z \right| = a$, then $z = \pm a$
$ \Rightarrow i + 2t = \pm 4$
$ \Rightarrow i = \pm 4 - 2t$
We know that the addition or subtraction of integers also results in an integer
Now as \[0 < t < 1\],
So, the only possible value of t for i to be an integer is $t = \dfrac{1}{2}$
$ \Rightarrow i = \pm 4 - 2\left( {\dfrac{1}{2}} \right)$
Simplifying the fractional part, we get,
$ \Rightarrow i = \pm 4 - 1$
i.e. $i = - 4 - 1$or $i = 4 - 1$
$\therefore i = - 5$ or $i = 3$
Now, we’ve $x = i + t$
Substituting the value of ‘i’ and ‘t’
i.e.$x = - 5 + \dfrac{1}{2}$ and $x = 3 + \dfrac{1}{2}$
$\therefore x = \dfrac{{ - 9}}{2}$and $x = \dfrac{7}{2}$
Therefore from the case I and case II we got 4 values of x i.e. $ \pm 4,\dfrac{{ - 9}}{2},\dfrac{7}{2}$
Option (B)4 is correct.

Note: Both the cases should be considered and all the possible values of x should be found.
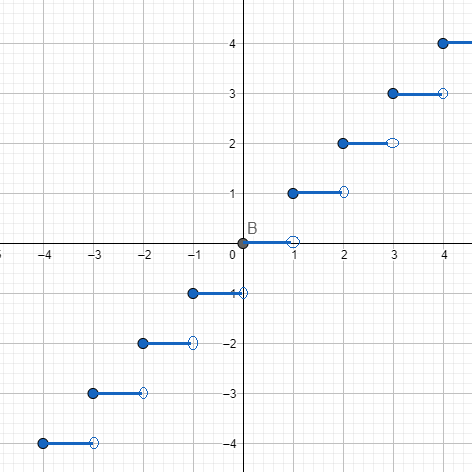
In the given solution we’ve talked about the greatest integer function [x]. Let us draw a graph of the greatest integer function for a better understanding of this function.
The greatest integer function is the function which gives us the value of integer greater or equal to the value inside the function