Question

The number of solution of \[{{\log }_{4}}\left( x-1 \right)={{\log }_{2}}\left( x-3 \right)\] is
A) \[3\]
B) \[1\]
C) \[2\]
D) \[0\]

Answer 1

Hint: To find the number of solution, first we need to determine the domain of the functions as to how far the solutions will go or be valid and after that we equate the L.H.S with R.H.S by dividing both the L.H.S and R.H.S with their respective log bases using the formula as:
\[{{\log }_{a}}\left( X \right)=\dfrac{\log X}{\log a}\]

Complete step-by-step answer:
First let us determine the value \[x\] is valid as you can see that one is \[x-1\] while other is \[x-3\] hence, the smallest values of \[x\] has to be \[3\] as any less than that we result in negative value for \[x-3\] and log of negative value is invalid. Hence, the L.H.S and R.H.S are valid for \x>3\.
\[{{\log }_{4}}\left( x-1 \right)={{\log }_{2}}\left( x-3 \right)\]
Using the conversion formula as: \[{{\log }_{a}}X=\dfrac{\log X}{\log a}\]
\[\dfrac{\log \left( x-1 \right)}{2\log 2}=\dfrac{\log \left( x-3 \right)}{\log 2}\]
Cross-multiplying the values we get:
\[\Rightarrow \dfrac{\log \left( x-1 \right)}{\log 2}=\dfrac{2\log \left( x-3 \right)}{\log 2}\]
\[\Rightarrow \dfrac{\log \left( x-1 \right)}{\log 2}=\dfrac{\log {{\left( x-3 \right)}^{2}}}{\log 2}\]
\[\Rightarrow \dfrac{\log \left( x-1 \right)}{1}=\dfrac{\log {{\left( x-3 \right)}^{2}}}{\log 2}\times \log 2\]
\[\Rightarrow \log \left( x-1 \right)=\log {{\left( x-3 \right)}^{2}}\]
Cancelling the log terms on both the sides
\[\Rightarrow \left( x-1 \right)={{\left( x-3 \right)}^{2}}\]
expanding the RHS using the $(a-b)^2$ formula
\[\Rightarrow x-1={{x}^{2}}-6x+9\]
Take all the terms to one side
\[\Rightarrow {{x}^{2}}-6x-x+9+1=0\]
\[\Rightarrow {{x}^{2}}-7x+10\]
\[\Rightarrow \left( x-5 \right)\left( x-2 \right)=0\]

The value of \[x\] is given as \[x=2,5\] and the domain is \[x>3\] therefore, the only value left is \[x=5\].

Note: Another method to find the number of solution is by graphical method, first draw the graphs \[{{\log }_{4}}\left( x-1 \right)\] (in red) and \[{{\log }_{2}}\left( x-3 \right)\] (in blue) and find the point/s where both the graph intersect. The graph intersects at \[x=4,x=2\]. As seen in the graph below:

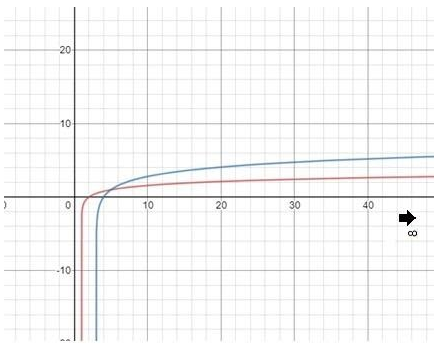
The only point where the graph intersects is \[\left( 5,1 \right)\].