Question

The number of real solutions \[{x^3} + {x^2} + 4x + 2\sin x = 0\] in \[0 \leqslant x \leqslant 2\pi \] is
a) four
b) two
c) one
d) 0

Answer 1

Hint: Here the given question is related to the algebraic equation and we have to find the number of the real solutions the equation has. The function contains the trigonometric function; it is highly impossible to find the root, so by plotting the graph we can determine the number of real roots the equation has.

Complete answer:
When we substitute the value of the x to the polynomial equation if we get a zero means then that value is considered as the root of the equation.
Now we consider the given question
\[{x^3} + {x^2} + 4x + 2\sin x = 0\]------ (1)
The highest power or degree of the above polynomial equation 3.
Consider the above polynomial equation as f(x), so we have
\[ \Rightarrow f(x) = {x^3} + {x^2} + 4x + 2\sin x\]
On differentiating the above function with respect to x, we get
\[ \Rightarrow f'(x) = 3{x^2} + 2x + 4 + 2\cos x\]
Here in this equation the domain of the x will be from 0 to \[2\pi \]
On substituting the value to the above equation then the value will be greater than 0.
The equation (1) can be written as
\[ \Rightarrow {x^3} + {x^2} + 4x = - 2\sin x\]
We consider \[{x^3} + {x^2} + 4x\] as one function and \[ - 2\sin x\] as a second function.
On plotting a graph for the above two function, it will be

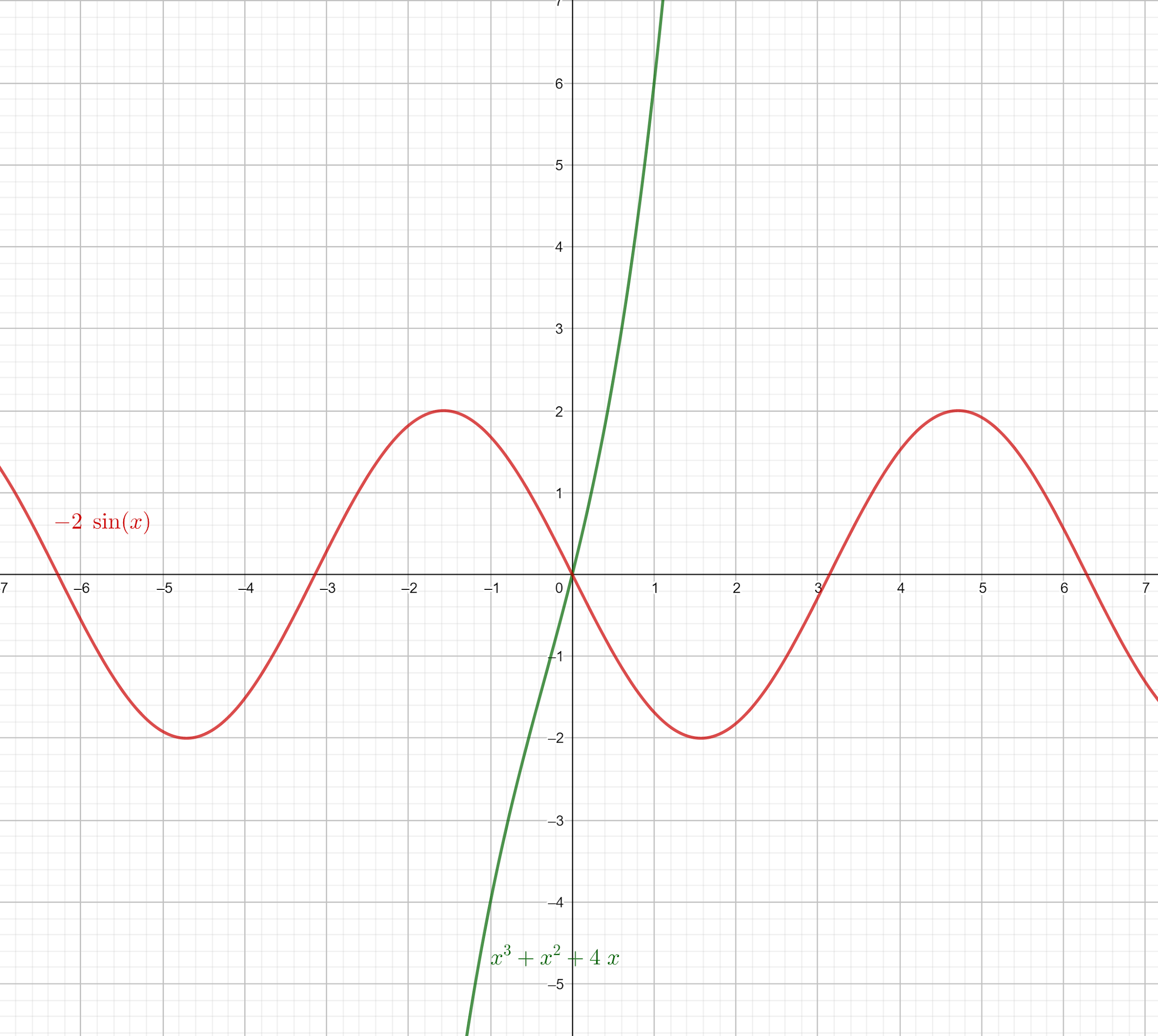
The graph of two functions will intersect at only one point. Therefore this indicates the polynomial equation.
Hence this equation has only one real root and that root will be a real one.
Therefore the option C is the correct one.

Note:
The number of the root will depend on the highest degree of the polynomial equation. The equation will have 3 roots but one root is real and the other two roots are imaginary. When we plot a graph for \[{x^3} + {x^2} + 4x + 2\sin x = 0\] we can’t determine the real root exactly so the separation of the algebraic equation and trigonometric function then it will be easy to determine the root.