Question

The number of matchsticks required to make 10 squares. The squares are placed one beside the other in an order.
A) 31
B) 20
C) 33
D) 32

Answer 1

Hint: Since four matchsticks will be required to make the first square. After that three matchsticks will be required to make the second square. Since one matchstick of the first square will be used as the $4^{th}$ side for the second square. Similarly, three matchsticks are required for the third square, and so on.

Complete step-by-step answer:
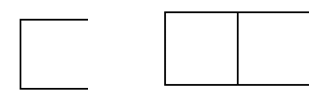
The first square will need four matchsticks. Consider the figure, the line represents the matchsticks.

For the second square take anyone matchstick as the one side of the second square. For the other three sides, three matchsticks are required, and so on.
The figure of two square is,

There are 7 lines which mean 7 matchsticks are required for two squares.
For the third square, again three matchsticks are required.
It is forming an Arithmetic Progression
$4,7,10, \ldots $
where, $a = 4$ and $d = 3$.
Now, find the 10th term of the A.P.,
As we know that ${a_n} = {a_1} + \left( {n - 1} \right)d$.
Put ${a_1} = 4,d = 3$ and $n = 10$. Then,
${a_{10}} = 4 + \left( {10 - 1} \right) \times 3$
Subtract 1 from 10 and then multiply the result with 3.
${a_{10}} = 4 + 27$
Now, add the terms to get the final answer,
${a_{10}} = 31$
Hence, the number of matchsticks required to make 10 squares is 31.

Option A is the correct answer.

Note: This question can be done in another way also.
If we remove one matchstick from the end, it will make a pattern of C’s.

So the number of matchsticks required for n C’s will be,
Number of C’s$ = 3n$
where n is the number of squares.
For square, 1 matchstick is required for the pattern of C’s.$$
Number of matchsticks required$ = 3n + 1$
Now, for 10 squares. Put $n = 10$,
So, the number of matchsticks required$ = 3 \times 10 + 1$
Multiply the terms and add 1 to it.
Number of matchsticks required$ = 31$
Hence, the number of matchsticks required is 31.