Question

The number of lines of symmetry in a divider is
(A) 0
(B) 1
(C) 2
(D) 3

Answer 1

Hint: Assume a divider BAC and draw its figure. We have to get the line of symmetry of the divider BAC. The line of symmetry is the line which will bisect \[\angle BAC\] and should have \[BA=AC\] .

Complete step-by-step answer:
According to the question, we have a divider and we have to find the number of lines of symmetry.
The line of symmetry is an imaginary line or an imaginary axis that passes through the center of the shape or an object and divides it into identical two parts or identical halves.
Here, we need the lines which can divide the divider into two equal parts in such a way that one part is exactly equal to the other part.
We have the divider and we have to divide it into two equal halves in such a way that all the parameters of one part should be equal to all the parameters of the second part.
Now, let us draw the figure of the divider,

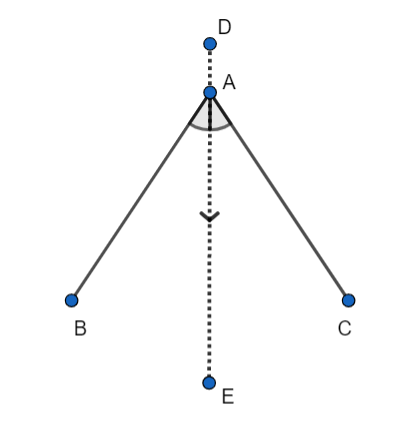
We can see that the line DE is dividing the divider BAC and we have two parameters here and the parameters are,
\[\angle BAE=\angle CAE\] ,
\[BA=AC\] .
Now, we can say that the line DE is dividing the divider and all the parameters of one part are equal to all the parameters of the second part.
We also don’t have any line other than the line DE which is dividing the divider in two equal parts.
Therefore, we can say that the line DE is the only line of symmetry for the divider BAC.
Hence, the correct option is (B).

Note: In this question, one can think of the line DE as shown in figure for the line of symmetry of the divider.
 

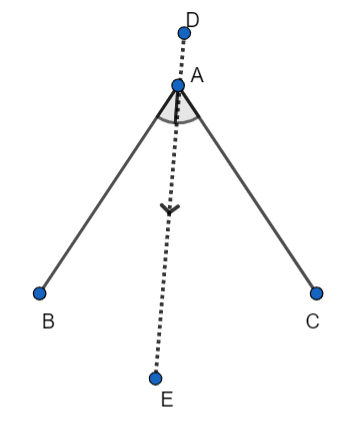
The line DE cannot be treated as the line of symmetry. We should have all the parameters equal. All the parameters of one part are not equal to all the parameters of the other part. Here, we have two parameters,
\[BA=AC\]
\[\angle BAE\ne \angle CAE\] .
Here, the angles are not equal.
So, the line DE is not a line of symmetry for the divider. For DE to be the line of symmetry, we should have \[\angle BAE=\angle CAE\] and \[BA=AC\] .