Question

The number of H+ ions in 1cc of a solution of \[pH = 13\] is:
A. \[6.023 \times {10^7}\]
B. \[1 \times {10^{ - 13}}\]
C. \[6.023 \times {10^{23}}\]
D. \[1 \times {10^{ - 16}}\]

Answer 1

Hint: \[pH\] is the scale of acidity or basicity of a solution. Recall the \[pH\] formula and you have to put values in it and you get the answer.

Complete step by step answer:
\[pH\] stands for Potential of Hydrogen or power of hydrogen. It is a scale used to specify the acidity or basicity of an aqueous solution. Acidic solutions have lower \[pH\] value than basic or alkaline solutions. \[pH\] is measured as the decimal logarithm of the reciprocal of the hydrogen ion activity.
 \[pH = - {\log _{10}}(a{H^ + }) = {\log _{10}}(\dfrac{1}{{a{H^ + }}})\]
Now, according to the equation we have \[pH\] value from which we can find the hydrogen ion activity. Therefore,
 \[[H + ] = {10^{ - 13}}\]
This means that \[1L\] of solution contains \[{10^{ - 13}}\] moles of hydrogen ions.
Hence, \[1cc\] or \[1ml\] of solution will contain
 \[{10^{ - 13}} \times \dfrac{1}{{1000}} = {10^{ - 16}}\] moles of hydrogen ions.
On multiplying it with Avogadro’s constant we get,
 \[{10^{ - 16}} \times 6.023 \times {10^{ - 23}} = 6.023 \times {10^7}\] hydrogen ions

Therefore, the correct option is A.

Additional information:
To measure the \[pH\] value we have a \[pH\] scale. The scale is as given below.

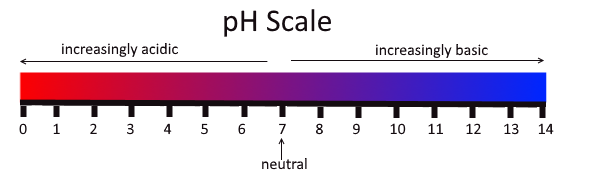
The range of the scale is from 0 to 14. \[pH\] value 7 means neutral solution. If \[pH\] is less than 7 then it is an acidic solution and \[pH\] more than 7 means the solution is basic. It is the measure of the relative amount of free hydrogen ions in the water.
The \[pH\] is very important as it tells many things about substances dissolved in it. For example the solubility of the compound and its biological availability and also of its constituents like nutrients. The amount that can be dissolved tells the toxicity of the water and mainly the substance present in it.

Note:
Taking care while calculations is important. Especially ones including powers and logarithms. There are chances of errors.