Question

The number of 5 digit telephone numbers having least one of their digits repeated.
a) 90,000
b) 100,000
c) 30,240
d) 69,760

Answer 1

Hint: At least one digit repeated numbers can be given by the difference of total numbers of 5 digits from the digits 0, 1, 2, 3, 4, 5, 6, 7, 8, 9. with allowed repetition and the numbers with no repetition (distinct digits). Selection of ‘r’ different things from the total ‘n’ different things is given by $ C_{r}^{n}=\dfrac{n!}{r!\left( n-r \right)!} $ . Arrangement of ‘r’ digit numbers from ‘n’ digits with allowed repetition is given as $ {{n}^{r}} $ .

Complete step-by-step answer:
As we know there are 10 digits 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 that can be used for making a 5 digit telephone number and as we need to determine total telephonic numbers of 5 digits having at least one digit repeated. It means there may be repetition of one digit or repetition of two digits or three but all the digits involved for making 5 digits cannot be distinct to each other i.e. at least one digit should be repeated.
So, in other words we need to calculate all the 5 digit numbers except the numbers which have all 5 digit different. It means total telephonic numbers with 5 digits having at least one digit repeated can be calculated by the difference of total numbers of 5 digits and the numbers with all distinct 5 digits. So, total 5 digit numbers with the help of 10 digit numbers and repetition is allowed with the formation of numbers can be given as

As digits can be repeated it means there are 10 possibilities for a single digit. Hence, total 5 digit numbers can be given as
 $ 10\times 10\times 10\times 10\times 10={{\left( 10 \right)}^{5}} $
Now, as we know, selection of r different things from ‘n’ different numbers is given by relation $ C_{r}^{n}=\dfrac{n!}{r!\left( n-r \right)!} $ . Hence, we can select 5 different digits from the total 10 digits i.e. 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 by $ C_{5}^{10} $ ways. Now, we need to arrange these digits to get the total number of 5 digits.
Now, as we know that the total 5 digit numbers with no repetition can be calculated as

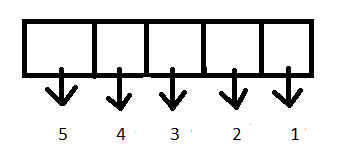
The first digit can be filled by 5 ways and second by 4 because the same digit cannot be occupied at two places as repetition is not allowed. Similarly, 3^rd place can be filled by 3 ways as two digits are already occupied with two different numbers. Hence, we can get total number of 5 digits telephonic number with 5 selected digits
 $ C_{5}^{10}\times 5\times 4\times 3\times 2\times 1=C_{5}^{10}\times 120 $
So, numbers with at least one digit repeated are given by the difference of total numbers possible with repetition and without repetition. So, we get total 5 digit telephone numbers with having at least one of the digit repeated
 $ {{\left( 10 \right)}^{5}}-C_{5}^{10}\times 5\times 4\times 3\times 2\times 1 $
= 100,000 – 30240
= 69760.
Hence, option (d) is correct.

Note: One may go wrong if he or she select 5 digits from the given numbers by $ C_{5}^{10} $ ways for the formation of numbers with repetition allowed case as $ C_{5}^{10} $ used for selecting 5 different numbers from 10 different numbers. So, don’t be confused with that part. One may use formula $ P_{r}^{n} $ for selecting 5 different digits and arranging them for the formation of numbers with distinct digits. As $ P_{r}^{n} $ gives selection and arrangement both at a time. So, it can be another approach for this step in the solution.
One may arrange the 5 different digits by 5! Ways directly for the second case in the solution. The arrangement of ‘n’ different things can be given by formula n!.