Question

The normal at the point $\left( at_{1}^{2},2a{{t}_{1}} \right)$ meets the parabola again in the point $\left( at_{2}^{2},2a{{t}_{2}} \right)$ , prove that ${{t}_{2}}=-{{t}_{1}}-\dfrac{2}{{{t}_{1}}}$.

Answer 1

Hint: To establish the relation between ${{t}_{1}}$ and ${{t}_{2}}$ . Find the equation of the normal at point $P\left( at_{1}^{2},2a{{t}_{1}} \right)$ .Now put $Q\left( at_{2}^{2},2a{{t}_{2}} \right)$ in this equation. Simplify the equation using basic formulas and prove the relation given.

Complete step-by-step answer:
It is said that the normal at the point $\left( at_{1}^{2},2a{{t}_{1}} \right)$ meets the parabola again in the point $\left( at_{2}^{2},2a{{t}_{2}} \right)$.
Let cut the equation of parabola ${{y}^{2}}=4ax$ .

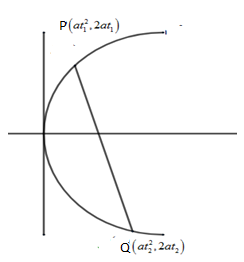
Let the 2 point on the parabola be $P\left( at_{1}^{2},2a{{t}_{1}} \right)$ and $Q\left( at_{2}^{2},2a{{t}_{2}} \right)$ .
We need to establish the relation between ${{t}_{1}}$ and ${{t}_{2}}$ .
Normally a point P is given by the equation $y=-{{t}_{1}}x+2a{{t}_{1}}+at_{1}^{3}$ . We know $Q\left( at_{2}^{2},2a{{t}_{2}} \right)$ , thus this point should be able to satisfy the equation. Put $y=2a{{t}_{2}}$ and $x=at_{2}^{2}$ in the above equation. Thus we get-
$2a{{t}_{2}}=-{{t}_{1}}\left( at_{2}^{2} \right)+2a{{t}_{1}}+at_{1}^{3}$
Now let us simplify this above equation.
The equation of normal for the general equation parabola ${{y}^{2}}=4ax$ is given as,
$y-{{y}_{1}}=\dfrac{-{{y}_{1}}}{2a}\left( x-{{x}_{1}} \right)$ .
Now let us find the equation of normal for point $P\left( at_{1}^{2},2a{{t}_{1}} \right)$. Thus, put $x=at_{1}^{2}$ and ${{y}_{1}}=2a{{t}_{1}}$ in the above equation.
$y-2a{{t}_{1}}=\dfrac{-2a{{t}_{1}}}{2a}\left( x-at_{1}^{2} \right)$
Now cancel out the like terms and simplify the above expression,
$\begin{align}
  & y-2a{{t}_{1}}=-{{t}_{1}}\left( x-at_{1}^{2} \right) \\
 & y-2a{{t}_{1}}=-x{{t}_{1}}+at_{1}^{3} \\
 & \Rightarrow y=-{{t}_{1}}x+at_{1}^{3} \\
\end{align}$
Normally a point P is given by the equation $y=-{{t}_{1}}x+2a{{t}_{1}}+at_{1}^{3}$ . We know $Q\left( at_{2}^{2},2a{{t}_{2}} \right)$ , thus this point should be able to satisfy the equation. Put $y=2a{{t}_{2}}$ and $x=at_{2}^{2}$ in the above equation. Thus we get-
$2a{{t}_{2}}=-{{t}_{1}}\left( at_{2}^{2} \right)+2a{{t}_{1}}+at_{1}^{3}$
Now let us simplify this above equation.
$\begin{align}
  & 2a{{t}_{2}}=-a{{t}_{1}}t_{2}^{2}+2a{{t}_{1}}+at_{1}^{3} \\
 & \Rightarrow at_{2}^{2}{{t}_{1}}-at_{1}^{3}=2a{{t}_{1}}-2a{{t}_{2}} \\
 & a{{t}_{1}}\left( t_{2}^{2}-t_{1}^{2} \right)=2a\left( {{t}_{1}}-{{t}_{2}} \right) \\
 & a{{t}_{1}}\left( t_{2}^{2}-t_{1}^{2} \right)-2a\left( {{t}_{1}}-{{t}_{2}} \right)=0 \\
 & a{{t}_{1}}\left( {{t}_{2}}-{{t}_{1}} \right)\left( {{t}_{2}}+{{t}_{1}} \right)+2a\left( {{t}_{2}}-{{t}_{1}} \right)=0 \\
\end{align}$ (We know ${{a}^{2}}-{{b}^{2}}=\left( a+b \right)\left( a-b \right)$)
Take out $a\left( {{t}_{2}}-{{t}_{1}} \right)$ from both terms.
$a\left( {{t}_{2}}-{{t}_{1}} \right)\left[ {{t}_{1}}\left( {{t}_{2}}+{{t}_{1}} \right)+2 \right]=0$
Thus $a\left( {{t}_{2}}-{{t}_{1}} \right)=0$
\[\begin{align}
  & {{t}_{1}}\left( {{t}_{2}}+{{t}_{1}} \right)+2=0 \\
 & \Rightarrow {{t}_{1}}\left( {{t}_{2}}+{{t}_{1}} \right)=-2 \\
 & {{t}_{2}}+{{t}_{1}}=\dfrac{-2}{{{t}_{1}}} \\
 & \therefore {{t}_{2}}=-t-\dfrac{2}{{{t}_{1}}} \\
\end{align}\]
Thus, we provide that the normal at the point $\left( at_{1}^{2},2a{{t}_{1}} \right)$ meets the parabola again in the point $\left( at_{2}^{2},2a{{t}_{2}} \right)$ and we get ${{t}_{2}}=-{{t}_{1}}-\dfrac{2}{{{t}_{1}}}$ .

Note: If normal at the point $a{{t}_{1}}$ meets the parabola again at $a{{t}_{2}}$ then $a{{t}_{2}}=a{{t}_{1}}-\dfrac{2}{a{{t}_{1}}}$ , The point of intersection of the normal to the parabola ${{y}^{2}}=4ax$ , ${{t}_{1}}$ and ${{t}_{2}}$ are $\left( 2a+a\left( t_{1}^{2}+{{t}_{1}}{{t}_{2}}+t_{2}^{2} \right),-a{{t}_{1}}{{t}_{2}}\left( {{t}_{1}}+{{t}_{2}} \right) \right)$ .